最速上升法

運用回歸設計和回響曲面分析的方法來解決實驗工作者通過實驗尋找最佳的工藝條件，在實驗者所選定的一個小區域上運用回歸設計擬合線性回歸方程，用最速上升法向最佳區域逼近因子區域，通常，將此法重複使用若干次，就可達到最佳區域。

基本介紹

• 中文名：最速上升法
• 外文名：steepest ascent
• 所屬學科：數學
• 相反概念：最速下降法
• 套用：尋求最佳工藝條件等

基本介紹

類比解釋

回響曲面方法的概念可以用爬山來類比進行解釋。圖1是一座山的二維等高線圖，圖中山周圍的相同高度用等高線表示。山高逐漸上升，直到峰頂為止。與尋找山峰類似，回響曲面方法是試圖在一系列爬山試驗中找到最優的回響(Y)。調優運算、單純形法、隨機調優運算和最速上升法是到達峰頂的不同路徑。回響曲面是重要的輸入變數與諸X’s的一個相關輸出或回響Y之間關係的數學(或圖形)表示。等值的Y被描繪成等高線，就像山峰的等高線一樣。

圖1

詳細介紹

系統最優運行條件的初步估計常常遠離實際的最優點，在這種情況下，實驗者的目的是要快速地進入到最優點的附近區域，我們希望利用既簡單又經濟有效的實驗方法，當遠離最優點時，通常假定在x的一個小區域範圍內一階模型是真實曲面的合適近似。最速上升法是沿著回響有最大增量的方向逐步移動的方法，當然，如果求的是最小值，則稱為最速下降法，所擬合的一階模型是

與一階回響曲面相應的 的等高線，是一組平行直線，如圖2所示，最速上升的方向就是增加得最快的方向，這一方向平行於擬合回響曲面等高線的法線方向，通常取通過感興趣區域的中心並且垂直於擬合曲面等高線的直線為最速上升路徑，這樣一來，沿著路徑的步長就和回歸係數 成正比，實際的步長大小是由實驗者根據工序知識或其他的實際考慮來確定的。

實驗是沿著最速上升的路徑進行的，直到觀測到的回響不再增加為止，然後，擬合一個新的一階模型，確定一條新的最速上升路徑，繼續按上述方法進行，最後，實驗者到達最優點的附近區域，這通常由一階模型的擬合不足來指出，這時，進行添加實驗會求得最優點的更為精確的估計。

圖2

相關計算

回響曲面一階回歸模型可以表示為：

我們可以對一階回歸模型求導數，可以得最速上升的步長為，就可以知道每一個的步長：

最後找到最最佳化的回響曲面區域的Y。

方法步驟

利用最速上升法尋找最佳區域的步驟為：

(1)在變數 的某區域內，通過正交設計，擬合一個線性回歸方程；

(2)由擬合的線性回歸方程，找出最速上升路線；

(3)沿著這條上升路線進行一系列實驗，直到y的值不再明顯增大為止；

(4)在(3)中y值不再明顯增大的那一點的鄰域內重複(1)、(2)、(3)；

(5)當擬合的線性回歸方程不再顯著，y的曲面具有明顯的彎曲時，擬合二次回歸，進

而找出最佳條件。

基本代碼

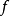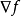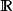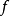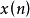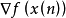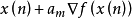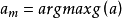執行最速上升法的基本代碼。假設 和 在 中的函式代碼已知，我們再假設已知函式line.search，此函式以 ， 和 為參數，返回值為 ，此處 (即使得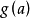 取得最大值的a值)。

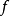
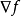
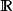
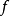
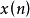
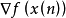
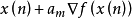
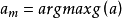
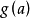
#Program spuRs/resources/scripts/ascent.r

source(“../scripts/linesearch.r”)

ascent<-function(f，grad.f，x0，tol=le-9，n.max=100){

# steepest ascent algorithm

# find a local max of f starting at x0

# function grad.f is the gradient of f

x<-x0

x.old<-x

X<-line．search(f，x，grad.f(x))

n<-1

while((f(x)-f(x.old>tol)&(n<n.max){

x.old<-x

x<-line.search(f,x,grad.f(x))

n<-n+1

}

return(x)

}