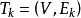最小樹形圖問題(shortest arborescence prob-lem)一類組合最佳化問題。若在最小樹問題中，將這個樹限定為樹形圖就變成了最小樹形圖問題。
基本介紹
- 中文名：最小樹形圖問題
- 外文名：Minimum tree problem
- 學科：數學、計算機科學
- 套用：數據結構、算法
前提,概念,解法,避圈法,破圈法,Kruskal 算法,
前提
樹形圖的概念
無圈且連通的無向圖稱為樹。樹一般記為T。作為樹定義還可以有以下幾種表述：
(1) T 連通且無圈或迴路；
(2) T 無圈且有n－1條邊（如果有n個結點）；
(3) T 連通有n－1條邊；
(4) T 無迴路，但不相鄰的兩個結點之間聯以一邊，恰得一個圈；
(5) T 連通，但去掉T 的任意一條邊，T 就不連通了；（亦即在點集合相同的圖中，樹是含邊數最少的
連通圖。）
(6) T 的任意兩個結點之間恰有一條初等鏈。
概念
一個網路圖可以有多個生成樹．記N的所有生成樹的集合為：
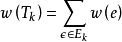
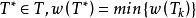
則稱 T * 為網路N的一棵最小樹樹形圖，簡稱最小樹。
解法
求最小樹的兩種方法，是避圈法與破圈法。
避圈法
從網路圖中任意節點開始尋找與該節點關聯的權數最小的邊，使之與已選邊不構成為圈，直到選夠n-1條邊為止。
避圈法破圈法
① 在網路圖中尋找一個圈。若不存在圈，則已經得到最短樹或網路不存在最短樹；
② 去掉該圈中權數最大的邊；
反覆重複 ① ② 兩步，直到最小樹。
破圈法Kruskal 算法
將圖中所有邊按權值從小到大排列，依次選所剩最小的邊加入邊集 T，只要不和前面加入的邊構成迴路，直到 T 中有 n-1 條邊，則 T 是最小生成樹。
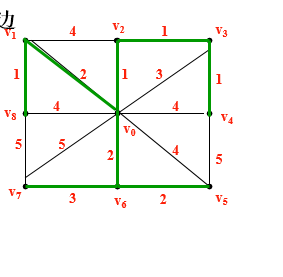Kruskal 算法