最小二乘濾波亦稱無系統參數的最小二乘配置.由觀測數據確定隨機參數最佳估值的一種方法.即在其函式模型中不包含非隨機參數的部分(參見“最小二乘配置”)。
最小二乘濾波(least squares filtering)亦稱無系統參數的最小二乘配置.由觀測數據確定隨機參數最佳估值的一種方法.即在其函式模型中不包含非隨機參數的部分(參見“最小二乘配置”).
濾波原是無線電工程中的一個術語.它本來的含義是從接收到的受干擾的電磁波信號中,排除噪聲的干擾,分離出所需要的信號.在一般的數據處理問題中,濾波就是通過含有誤差(噪聲)的觀測數據,確定隨機參數(信號)的最佳估值的方法.最小二乘濾波的線性函式模型為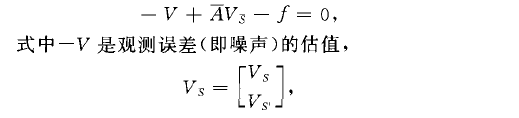
濾波原是無線電工程中的一個術語.它本來的含義是從接收到的受干擾的電磁波信號中,排除噪聲的干擾,分離出所需要的信號.在一般的數據處理問題中,濾波就是通過含有誤差(噪聲)的觀測數據,確定隨機參數(信號)的最佳估值的方法.最小二乘濾波的線性函式模型為
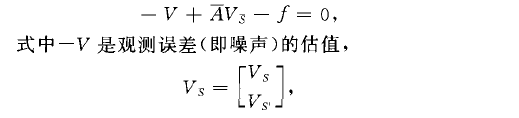
v、是觀測點信號s的改正數向量,v、是未測點信號S'的改正數向量,f是常數項,A= [A 0}是已知
的係數陣.
信號S和S'是隨某種因素變化的隨機函式向量,用以描述它們隨機性質的協方差陣,其元素的大小可由協方差函式確定.根據廣義最小二乘準則
VT P V +V歹P}Vfi=min
解出V和
廠V.s]
V;一I__一I
匕V.s,J
從而求得信號的估值S=S+V:和夕=S'+VS}. P 和屍:分別是觀測誤差(噪聲)和信號的先驗權陣.
的係數陣.
信號S和S'是隨某種因素變化的隨機函式向量,用以描述它們隨機性質的協方差陣,其元素的大小可由協方差函式確定.根據廣義最小二乘準則
VT P V +V歹P}Vfi=min
解出V和
廠V.s]
V;一I__一I
匕V.s,J
從而求得信號的估值S=S+V:和夕=S'+VS}. P 和屍:分別是觀測誤差(噪聲)和信號的先驗權陣.
