網際網路梅森素數大搜尋(GIMPS)項目宣布發現第 51 個梅森素數和已知最大的素數:2^82,589,933-1,共有 24,862,048 位。發現者是 GIMPS 志願者 Patrick Laroche,時間是在 2018 年 12 月 7 日。
基本介紹
- 中文名:最大素數
- 意義:目前發現的數值最大的素數
- 發現日期:2018年12月
- 數值:p=2^82,589,933-1
最大素數的發展,梅森素數,雲計算的最大素數,素數無限,
最大素數的發展
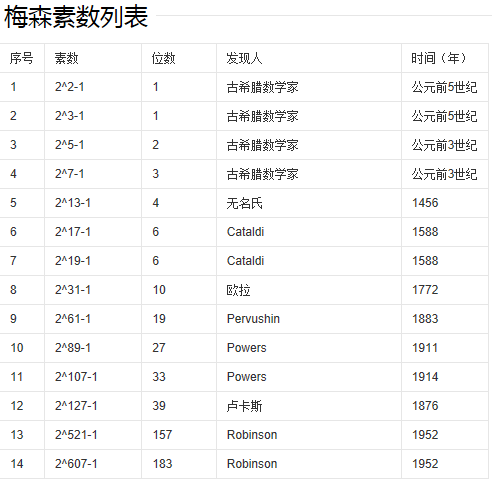
素數也叫質數,是只能被自己和1整除的數。按照規定,1不算素數,最小的素數是2,其後依次是3、5、7、11等等。 早在2500年前,希臘數學家歐幾里德就證明了素數是無限的,並提出少量素數可寫成“2的n次方減1(2^n-1)”的形式,這裡n也是一個素數。但是目前人類已知的素數很有限,因為數字越大,要發現新的素數就越困難。不過,很多數學家曾對素數問題進行過研究,17世紀的法國教士馬丁·梅森就是其中成果較為卓著的一位,因此後人將“2的n次方減1(2^n-1)”形式的素數稱為梅森素數。隨後,以梅森素數的形式,最大素數的記錄被不斷刷新。
1876年,數學家盧卡斯證明了2^127-1是當時已知的最大素數。這個記錄保持了75年,這是一個39位的數。
直到1951年,藉助於新出現的電子計算機,人們才發現有79位數字的更大素數。1952年時,最大素數是2^2,281-1,有687位數。位數在1,000位以上的素數到1961年才被發現,它是2^4,423-1,共有1332位數。從1951年到1971年的20年間,最大素數的紀錄被不斷刷新。1971年,美國數學家塔克曼在紐約州的紐克頓利用國際商業機器公司的IBM360/91型電子計算機,歷時39分26.4秒,算出了當時的最大素數2^19,937-1,這是一個6,002位的數字,它最前面的五位數是43,154,最後面的三位數是471。
1978年10月,世界幾乎所有的大新聞機構(包括中國的新華社)都報導了以下訊息:兩名年僅18歲的美國高中生諾爾和尼科爾使用CYBER174型計算機找到了第25個梅森素數:M21701。
2008年8月,美國加州大學洛杉磯分校(UCLA)的計算機專家史密斯(E.Smith)通過參加了一個名為“網際網路梅森素數大搜尋”(GIMPS)的國際合作項目,發現了第46個也是最大的梅森素數2^43,112,609-1,該素數也就是2自身相乘43,112,609次減1,它有12,978,189位數,如果用普通字號將這個巨數連續寫下來,它的長度可超過50公里!最近,這一成就被美國的《時代》雜誌評為“2008年度50項最佳發明”之一,排名在第29位。
據英國《新科學家》雜誌網站報導,美國中央密蘇里大學數學教授柯蒂斯·庫珀(Curtis Cooper)領導的研究小組於2013年1月25日發現了已知的最大梅森素數——2^57,885,161-1 (即2的57,885,161次方減1);該素數有17425170位,如果用普通字號將它連續列印下來,它的長度可超過65公里!
據外媒報導,美國州立中密蘇里大學柯蒂斯庫珀(Curtis Cooper)通過GIMPS項目發現了第49個梅森素數 2^74,20,7281-1(被稱為M74207281),為GIMPS項目誕生20周年獻禮。
2017年12月26日,網際網路梅森素數大搜尋(GIMPS)項目宣布發現第 50 個梅森素數和已知最大的素數:2^77,232,917-1,共有 23,249,425 位。該素數已被多人使用不同的硬體和軟體完成驗證。發現者是 GIMPS 志願者 Jonathan Pace,他住在田納西州的 Germantown,是一位電機工程師,他有資格獲得 3000 美元的研究發現獎。GIMPS 是一個分散式計算項目,至今已有 20 年歷史,它利用志願者的空閒 CPU 創建了一個遍布全球的超級計算機,它的 prime95 軟體此前發現了英特爾處理器的一個漏洞。
2018年12月7日,住在美國佛羅里達州奧卡拉市的Patrick Laroche也是通過GIMPS項目發現了第51個梅森素數:2^82,589,933-1(被稱為M82589933),共有24,862,048位。
梅森素數
序號 | 素數 | 位數 | 發現人 | 時間 |
51 | 2^82,589,933-1 | 24,862,048 | Patrick Laroche | 2018 |
50 | 2^77,232,917-1 | 23,249,425 | Jonathan Pace | 2017 |
49 | 2^74,207,281-1 | 22,338,618 | CurtisCooper | 2016 |
48 | 2^57,885,161-1 | 17,425,170 | Curtis Cooper | 2013 |
47 | 2^43,112,609-1 | 12,978,189 | Edson Smith | 2009 |
46 | 2^42,643,801-1 | 12,837,064 | Odd M. Strindmo | 2009 |
45 | 2^37,156,667-1 | 11,185,272 | Hans-Michael Elvenich | 2008 |
44 | 2^32,582,657-1 | 9,808,358 | Curtis Cooper及Steven Boone | 2006 |
43 | 2^30,402,457-1 | 9,152,052 | Curtis Cooper及Steven Boone | 2005 |
42 | 2^25,964,951-1 | 7,816,230 | Martin Nowak | 2005 |
41 | 2^24,036,583-1 | 7,235,733 | John Findley | 2004 |
40 | 2^20,996,011-1 | 6,320,430 | Michael Shafer | 2003 |
39 | 2^13,466,917-1 | 4,053,946 | Michael Cameron | 2001 |
38 | 2^6,972,593-1 | 2,098,960 | Nayan, Woltman, Kurowski | 1999 |
37 | 2^3,021,377-1 | 909,526 | Clarkson, Woltman, Kurowski | 1998 |
36 | 2^2,976,221-1 | 895,932 | Spence, Woltman | 1997 |
35 | 2^1,398,269-1 | 420,921 | Armengaud, Woltman | 1996 |
34 | 2^125,7787-1 | 378,632 | Slowinski & Gage | 1996 |
33 | 2^859,433-1 | 258,716 | Slowinski & Gage | 1994 |
32 | 2^756,839-1 | 227,832 | Slowinski & Gage | 1992 |
31 | 2^216,091-1 | 65,050 | David Slowinski | 1985 |
30 | 2^132,049-1 | 39,751 | David Slowinski | 1983 |
29 | 2^110,503-1 | 33,265 | Welsh & Colquitt | 1988 |
28 | 2^86,243-1 | 25,962 | David Slowinski | 1982 |
27 | 2^44,497-1 | 13,395 | Slowinski & Nelson | 1979 |
26 | 2^23,209-1 | 6,987 | L. Curt Noll | 1979 |
25 | 2^21,701-1 | 6,533 | Nickel & Noll | 1978 |
24 | 2^19,937-1 | 6,002 | Bryant Tuckerman | 1971 |
23 | 2^11,213-1 | 3,376 | Donald B. Gillies | 1963 |
22 | 2^9,941-1 | 2,993 | Donald B. Gillies | 1963 |
21 | 2^9,689-1 | 2,917 | Donald B. Gillies | 1963 |
20 | 2^4,423-1 | 1,332 | Alexander Hurwitz | 1961 |
19 | 2^4,253-1 | 1,281 | Alexander Hurwitz | 1961 |
雲計算的最大素數
1995 年,美國程式設計師喬治·沃特曼整理有關梅森素數的資料,編制了一個梅森素數計算程式,並將其放置在網際網路上供數學愛好者使用,這就是分散式計算網際網路梅森素數大搜尋(GIMPS)項目。目前有6萬多名志願者、超過20萬台計算機參與這項計畫。該計畫採取分散式計算方式,利用大量普通計算機的閒置時間,獲得相當於超級計算機的運算能力,第 37、38 和 39 個梅森素數都是用這種方法找到的。美國一家基金會還專門設立了 10 萬美元的獎金,鼓勵第一個找到超過千萬位素數的人。
素數無限
不存在最大質數!
上國小的時候,我們就知道所有的正整數可以分為質數(素數)和合數兩類,當然還特別規定了“1既不是質數,也不是合數”。100以內的質數,從小到大依次是:2、3、5、7、11、13、17、19、……、83、89、97。不用說了,你一定背不下來。那么質數的個數是不是有限多的呢?
(附:100以內的質數從小到大依次是:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61, 67,71,73,79,83,89,97。總計25個。)
在解決這個問題之前,我們先來看看另一個問題:怎樣判斷一個已知自然數是不是質數。比如,143是不是質數?
你一定會按照下面這個步驟去判斷: 先用最小的質數2去除143,不能整除;再用3去試試,還是不行;再依次用5、7試試,還是不行;11呢?行!143=11×13,所以143不是質數,而是合數。所以,判斷一個數是不是質數,只需用比這個數小的所有質數,依次去除它即可,如果都不能整除的話,這個數就一定是質數;相反,只要這個數能夠被某一個質數整除,這個數就一定是合數。這種方法所依據的原理是:每一個合數都可以表示成若干個質數的乘積。不用說,這叫做“分解質因數”,也是國小數學的知識。
我們先假設質數的個數是有限多的,用p1,p2,……,pn表示,那么必然存在一個“最大的質數”,設這個“最大的質數”為pn。下面我們找出從1到pn之間的所有質數,把它們連乘起來,就是:
2×3×5×7×11×13×……×pn,設為N
把這個連乘積再加上1,得到一個相當大的數M:
M=2×3×5×7×11×13×……×pn+1,即M=N+1;
那么這個M是質數還是合數呢?
如果M為質數,因M要大於p1,p2,……,pn,所以它不在那些假設的全部素數的集合中。
如果M為合數,因為任何一個合數都可以分解為幾個素數的積;而N和M(N+1)的最大公約數是1,所以M不可能被p1,p2,……,pn整除,所以該合數分解得到的素因數肯定不在假設的全部素數的集合中。
因此無論該數是素數還是合數,都意味著在假設的有限個素數之外還存在著其他素數。所以原先的假設不成立。也就是說,素數有無窮多個。