基本介紹
- 中文名：最佳化截取內嵌碼塊編碼
- 外文名：embedded block coding with optimized truncation
- 簡稱：EBCOT
- 提出者： David Taubma
- 套用：圖像編碼
- 組成結構：塊編碼和碼流組織
JPEG2000 的基本結構,EBCOT簡介,EBCOT 的優點,比特平面編碼,原理,具體算法步驟,算術編碼,率失真最最佳化算法,
JPEG2000 的基本結構
JPEG2000 的基本結構如圖1所示。首先對原始圖像數據預處理，接著進行離散小波變換，然後在形成輸出碼流(比特流)之前，對變換係數進行量化、比特平面編碼和算術解碼，最後進行率失真控制和碼流組織，形成壓縮碼流。壓縮碼流通過存儲或傳輸後，進行與上述過程相反的變換後恢復出圖像數據。
EBCOT簡介
EBCOT 算法是建立在碼塊(code-block)的基礎上，將每個子帶分成若干塊，如 32x32 或 64x64，每個碼塊獨立編碼，利用內部的相關特性進行壓縮，對於每個碼塊再按質量進行分層，分成若干塊段，各個塊段之間就是截斷點；選擇一些碼塊和碼塊中的一些碼段，就可以支持多解析度和質量的碼流結構。
EBCOT 算法可以分為 T1 和 T2 兩部分，圖2所示。T1包括比特平面編碼、算術編碼，負責數據的具體壓縮；T2負責碼流組織，主要根據壓縮後率失真最最佳化算法(PCRD)實現的碼流進行組織，並完成最後的打包工作。
EBCOT 的優點
(1) 定質量解釋：由於每個質量層可包含來自每個碼塊的任意貢獻，質量的概念容易適應面向特定套用的顯著性量度。與EZW和SPIHT和其他嵌入式壓縮算法相比，當已知對應的空間區域或頻帶對某個套用並不重要時，EBCOT允許截斷不需要的質量層數據。
(2) 靈活的結構：EBCOT 具有解析度可伸縮性、失真可伸縮性(只要採用多重質量層)和一定程度的空間可伸縮性。當壓縮多重圖像分量(例如，彩色分量)時，這些分量構成了可伸縮性的第四維。JPEG2000 支持所有沿四維的漸進。
(3) 局部處理：獨立編碼允許對每個碼塊中的樣本進行局部處理，這有利於硬體的實現。獨立編碼引入高度並行實現的可能性，其中多個碼塊可以同時進行編碼和解碼。
(4) 有效壓縮：PCRD(壓縮後率失真最佳化)算法可以更多的補償由於施加獨立塊編碼產生的效率損失，算法也能夠適應空間變化和與圖像有關的失真度量。
(5) 抗誤碼：在任何塊編碼的位流中遇到的誤差對其他塊編碼沒有影響，即所有JPEG2000 的碼流都是解析度可分割的。
比特平面編碼
原理
比特平面編碼的任務就是生成數據的上下文信息，以供熵編碼使用。它以碼塊為單位，掃描方式如圖3所示。在某一比特平面上，一列中 4 個相鄰的點組成一個條帶。算法從第一個點(左上角)開始,依次掃描當前條帶內的 4 個點，然後跳到右側相鄰條帶，掃描到碼塊的右側邊界時，折回到左側的下一條帶。
碼塊的每個比特平面要經過 3 道掃描。重要性傳播過程(SignificancePropagation Pass)，使用零編碼 ZC 和符號編碼 SC 原語編碼；幅度細化過程(Magnitude Refinement Coding )，使用 MRC 原語編碼；清理過程(Clear Pass )，使用遊程編碼 RLC 和符號編碼 SC 原語編碼。
很多情況下，子帶的小波係數的高位比特平面出現全零的情況，編碼從最高重要比特平面 MSB 開始可節約大量時間。每層比特平面按 3 道掃描順序處理完該比特平面，然後再用同樣的方法處理低一層的比特平面，直到第 0 比特平面處理完成，表明該碼塊的比特平面編碼完成。
具體算法步驟
具體的比特平面編碼算法如下：
(1) 重要性傳播，
：對於自己不重要但有重要鄰居的係數進行ZC編碼，如果係數由不重要變成重要則進行SC 編碼。
(2) 幅值細化，
：對於己經重要的且在當前比特平面沒有編碼的係數進行MR編碼。
(3) 清理更新，
：對於自己不重要且未編碼過的係數進行ZC或RLC 編碼，如果有係數由不重要變成重要則進行SC 編碼。這裡又引入一個訪問狀態變數ηi[m,n]來表示
在當前比特平面是否編碼過。
(4) ηi[m,n]置0，返回第1步進行下一個比特平面p-1的編碼。
算術編碼
算術編碼是一種用於數據壓縮的編碼技術，它是基於 Shannon 定理的可變長的熵編碼。算術編碼的基本思想是用區域劃分來表示信源輸出序列，信源輸出的任何一種組合，與[0 ,1) 區間內的某一區域一一對應。用算術方法表示這一區域為一個二進制小數。這個二進制小數是信源輸出序列的一種編碼，且它是唯一可解碼的。算術編碼的編碼過程與信源的機率模型是分離的。在實際中使用機率估值表。
率失真最最佳化算法
T1編碼器產生的比特流是內嵌的，利用率失真最佳化截取算法可以獲得最優的壓縮性能。設碼塊
在T1部分產生的內嵌比特流的碼率截止到
，
是某個截取點，即T1某個編碼過程的結束點，則圖像總的碼率為：
設碼塊
的係數在恢復圖像中產生的失真為
且其失真是加性的，即：
其中，D表示整幅圖像的失真大小。
現在需要找到一組
，使得在滿足
時，D最小。解決這種條件極值問題可以通過拉格朗日算法。因此問題等價於使下式最小化：
其中調整
直到產生一組截取點使得上式在滿足
時最小。對於上式最小化問題很可以歸結為單個碼塊的最小化問題。即對於碼塊
找到截取點
使得
最小。查找算法如下：
(1) 令
=0(即沒有比特流)；
(2) 對於k=1,2,3…，計算
，
；
(3) 若
，則
=k。
由於這個算法要對不同的
進行查找，因此先剔除一些奇異點，使率失真斜率
隨著k嚴格單調減。確定候選截取點算法如下：
(1) 令
={n}，n∈N，即所有過程的截止點；
(2) 令p=0；
(3) 對於 k，k∈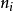
。
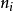
計算
，
，
。若p≠0且
，則從
剔除p並返回(2)；否則，令p=k。
