晶帶是指從晶體外形引出的。兩個晶面相交於一個晶棱,當晶面相交的棱彼此平行時,所有這些晶面構成一個晶帶。
在晶面之間凡相交或平行於同一晶向直線的各晶面組,構成一個晶帶。這組晶面叫共帶面,該直線稱為此晶帶的晶帶軸。同一晶帶中所有晶面的共同特點是:所有晶面的法線都與晶帶軸垂直。由於同一晶帶中所有晶面均與晶帶軸相平行。
基本介紹
概述,晶帶軸,晶帶定律,
概述
晶帶是指這樣的一組晶面,各晶面的法線方向垂直於同一根軸,或晶面相交的晶棱互相平行,見下圖,(h1k1l1)、(h2k2l2)、(h3k3l3)為3個晶面,通過同一根軸,其法線分別為N1、N2、N3,顯然三法線共面於平面P,這根軸即為晶帶軸。晶帶軸是表示晶帶方向的一根直線.它平行於該晶帶的所有晶面,也是該晶帶所有晶面的公共棱。晶面採用晶帶軸指數[u v w]來表征。
所有相交於某一晶向直線或平行於此直線的晶面構成一個晶帶,此直線稱為晶帶軸,這些晶面是屬於此晶帶的面,稱為共帶面。由於任何兩個不平行的晶面必然相交,其交線即是晶帶軸,此兩晶面即屬該晶帶的晶面,故晶帶可有很多,但通常用到的是那些有著許多晶面的晶帶,如上述的[001]晶帶軸的晶帶等。
晶帶軸[u v w]與該晶帶的晶面(hkl)之間存在以下關係:hu+kv+lw=0
凡滿足此關係的晶面都屬於以[u v w]為晶帶軸的晶帶,故此關係式也稱作晶帶定律。此外,如果有兩個不平行的晶面(h1k1l1)和(h2k2l2),則其晶帶軸[u v w]可從下式求得:
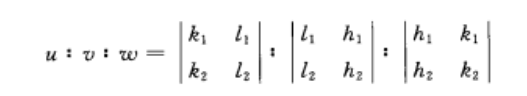 晶帶公式
晶帶公式或寫成如下形式:
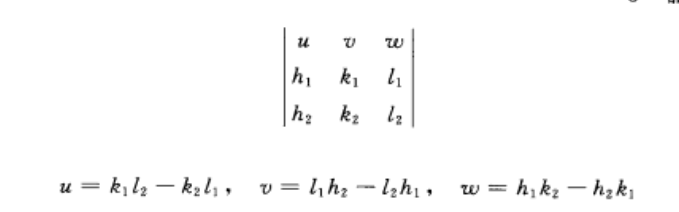 晶帶公式
晶帶公式晶帶是指彼此問的交棱均相互平行的一組晶面之組合。這裡所指的交棱,既包括在晶體上已經相交而存在的實際晶棱,也包括實際並未相交,但延展晶面後,即可相交的可能晶棱。從而,一個晶帶的各個晶面,即可彼此連線而構成封閉的環帶分布。
晶帶軸
晶帶軸是指在同一晶帶中所有晶面與其他面的交線互相平行,其中通過坐標原點的那條平行直線稱為晶帶軸。晶帶軸表示了晶帶中各類晶面分布的特徵,常以晶帶軸作為晶帶的標誌,以晶帶軸的方向指數表示該晶帶的指數。晶帶概念用於點陣時,平行於某一點陣直線的所有陣點平面的總體稱為晶帶,該點陣直線是晶帶軸。
晶帶定律
晶帶定律(zone law)又稱魏斯定律(Weiss zone law),系由德國學者魏斯(Christian Samuel Weiss)於1805~1809年間所確定的。其內容為:晶體上的任一晶面至少同時屬於兩個晶帶,或者說,平行於兩個相交晶帶的公共平面必為一可能晶面。根據晶帶定律可知:由任意兩個互不平行的晶面即可決定一個晶帶,而由任意兩個晶帶又可決定一個晶面;從而,由互不平行的4個任意已知晶面(其中每3個均不屬於同一晶帶),或由任意4個已知晶棱(即晶帶軸,其中每3個均不共面),即可導出此晶體上一切可能的晶面和晶棱,並推算出相應的晶面符號和晶棱符號。
晶帶是指空間點陣中平行於同一晶軸的所有晶面。當該晶軸通過坐標原點時稱為晶帶軸.晶帶軸的晶向指數稱為晶帶指數。晶帶的概念在晶體衍射分析中非常重要。
由晶帶定義得,同一晶帶的所有晶面的法線均垂直於晶帶軸,晶帶軸可由正點陣的矢量R表示,即R=ua+vb+wc可由其倒易矢量表征。由此可得:
uh+vk+wl=0
該式表明晶帶軸的晶向指數與該晶帶的所有晶面的指數對應積的和為零。反過來,凡是屬於[u v w]晶帶的所有晶面(hkl),必須滿足該關係式。該關係即為晶帶定律。

