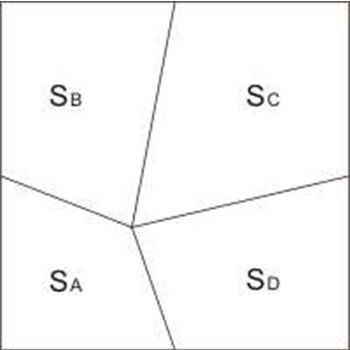
晏略殊定理:正方形內任意一點,向其各邊中點的連線,構成四個不規則的四邊形,其中相對的兩個四邊形面積之和等於另外兩個相對四邊形的面積之和。
基本介紹
- 中文名:晏略殊定理
- 外文名:Yanlueshu sheorem
- 表達式: SA+SC=SB+SD
- 提出者:晏略殊
- 適用領域:數學
證明,定理套用,整數冪個位數的數學命題,
證明
設:S1+S2 =SA ;S3+S4 =SB ;S5+S6 =SC; S7+S8 =SD
則:SA+SC=S1+S2+S5+S6;SB+SD=S3+S4+S7+S8
因為: S1=S8,S2=S3,S4=S5,S6=S7。
所以 SA+SC=S8+S3+S4+S7=SB+SD
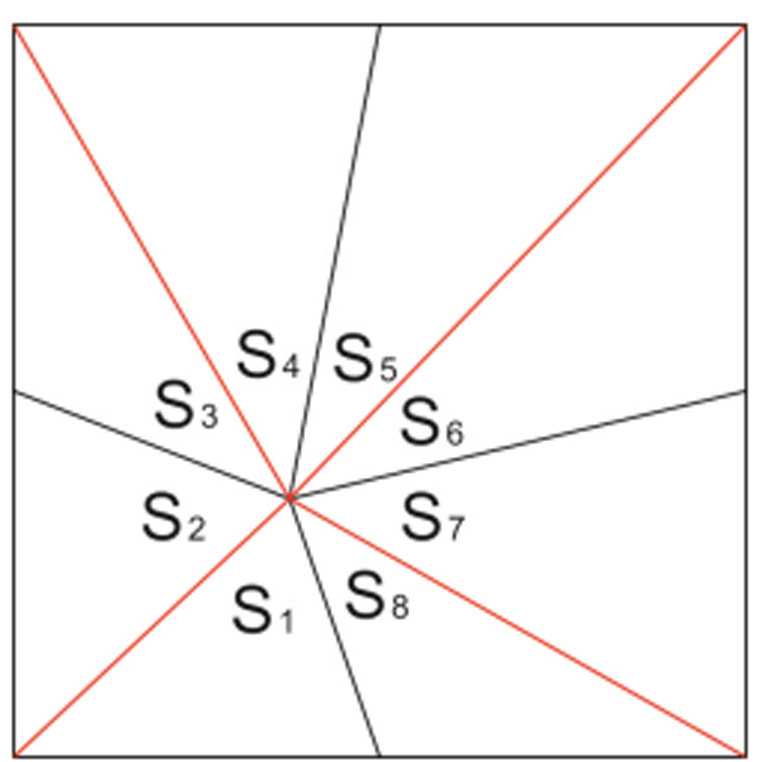
證明圖
定理套用
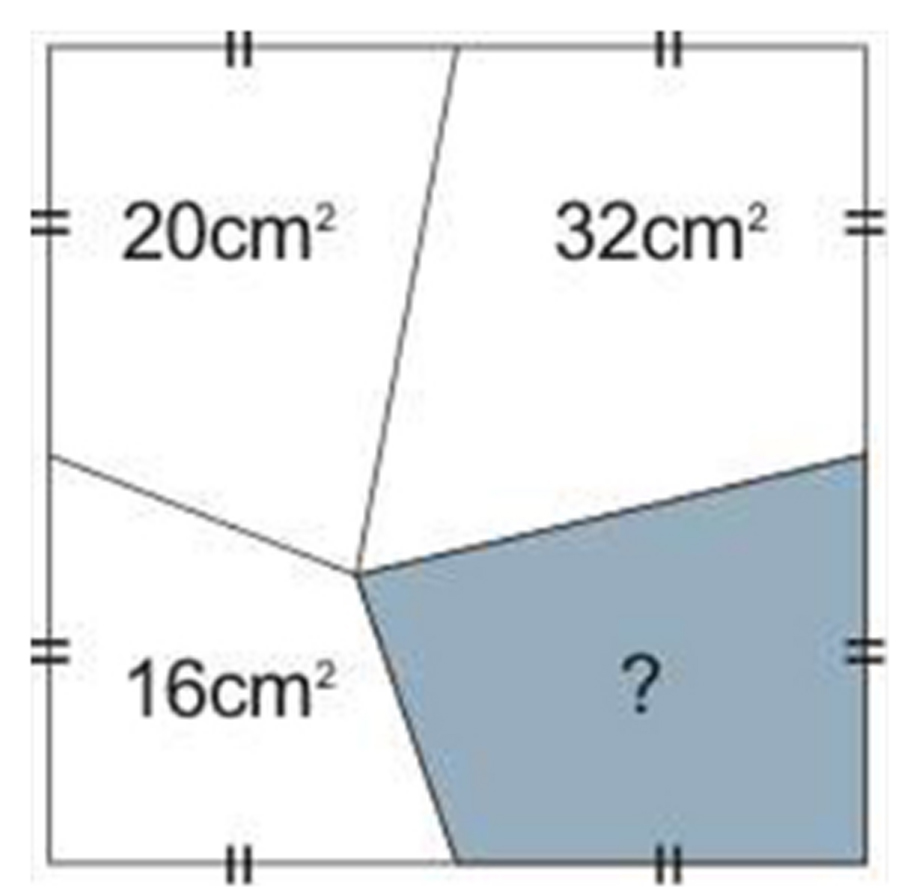
例題:已知正方形部分區域面積,求陰影?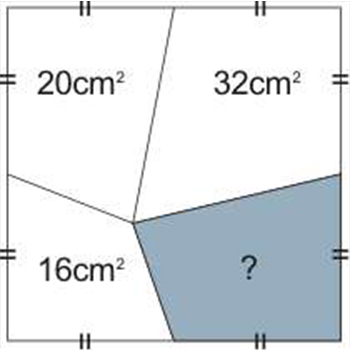

套用圖1
解法一(常規法):首先將四個四邊形分解為八個小三角形並設它們的面積分別為:S1,S2,S3,S4 ,S5,S6,S7,S8 。
在面積為S1的三角形內做垂線可以證明S1=S8
同理:S2=S3,S4=S5,S6=S7
因為S1+S2+S3+S4+S5+S6=16+20+32=68
所以S8+S2+S3+S4+S5+S7=68
S8+S3+S3+S4+S4+S7=68
S7+S8=68-40
S7+S8=28
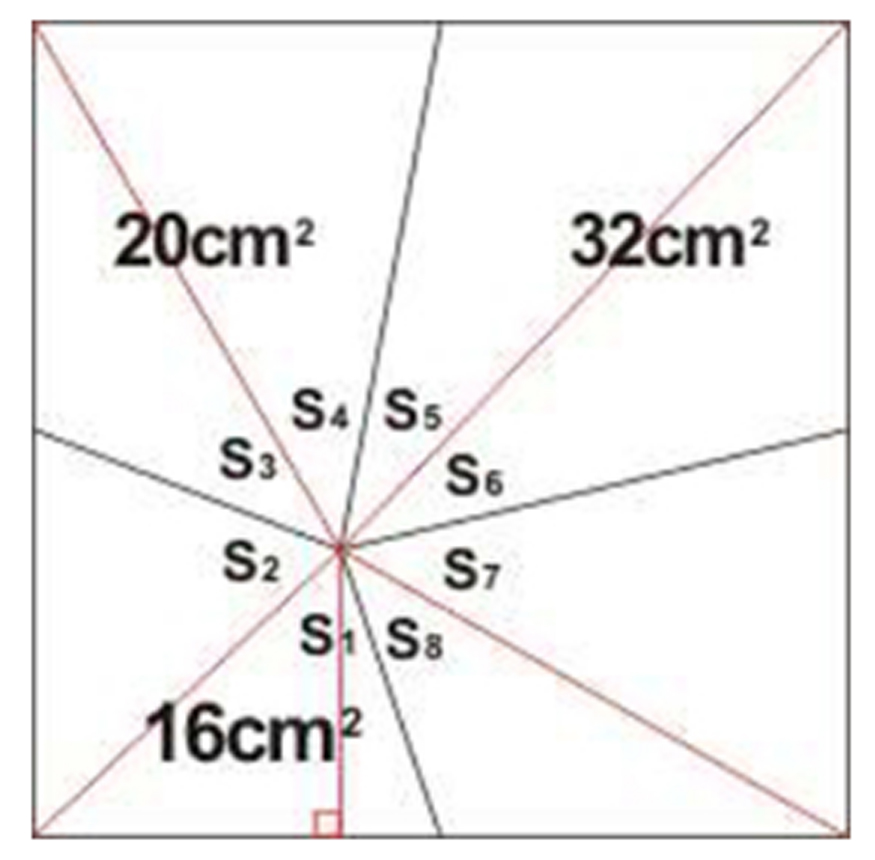
套用圖2
解法二(定理法): 設陰影四邊形面積為X,
則 20+X=16+32
X=28
套用圖3
整數冪個位數的數學命題
當整數A不等於零時,其5+4n(n為自然數)次冪的個位數等於原整數A的個位數或A本身。