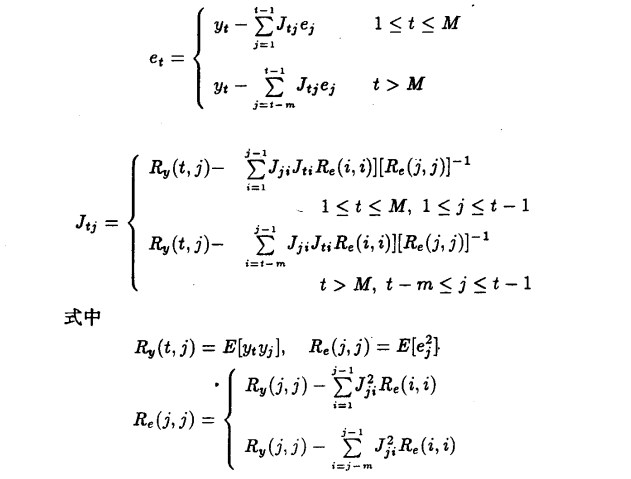新息定理

新息定理是新息預報的基礎。新息預報雖然公式較複雜，但占用的記憶體是有限的，並不隨t而增長，而且每步預報是用遞推計算，特別是MA序列，由新息預報公式可以看出，只要能判斷出MA模型的階數，不必計算出滑動平均參數就可以遞推進行新息預報。由新息定理可以看出，時刻t的新息e_t是隨著樣本數據x_t的輸入經過遞推而得到的。

基本介紹

• 中文名：新息定理
• 所屬學科：數學
• 所屬問題：統計學（時間序列）
• 簡介：新息定理是新息預報的基礎

新息預報的原理

ARMA序列的平穩預報是根據全部歷史數據x_t，x_t-1給出x_t+l(l>0)的線性最小方差預報 ，然而在實際問題中只能獲得有限的歷史資料。對於AR序列來說，用有限資料就可以對未來實現嚴格的平穩線性最小方差預報，而對於MA或ARMA序列，則只能給出 的近似值，且數據存貯及計算量隨時間t而增加。新息預報就是用有限歷史數據x_t，x_t-1，…，x₁對未來時刻x_t+l做的線性最小方差預報，與平穩預報相區別，相應的新息預報記為 。 根據新息定理： 設 {x_t} 為零均值平穩序列適合於ARMA (p，q) 模型，令M=max(p，q) 定義序列 {y_t} 為

一步預報誤差為e_t=x_t- ，把 看成是以前的“舊”數據x_t-1，x_t-2，…x₁所提供關於x_t的最大信息，e_t可以看做是從新的數據x_t中得到的最新信息，因此稱 {e_t} 為新息序列。e_t滿足如下遞推關係

其中

式中R_y(t，j) =E (y_ty_j)，R_e(j，j) =E ( )，且

步實時預報公式為

當 時取 ，以上各式中當求和上限小於下限時，約定求和值為零。從新息預報遞推公式可以看到每輸入一個新的觀察值x_t就可以遞推算出新預報值 。

相關分析及結論

除AR(p)模型外，平穩線性最小方差預報需要根據無窮個歷史數據來進行，然而實際問題中只能獲得有限資料；當q>0時只能得到 的近似值，且僅當k達到適當大之後，由近似所帶來的誤差才可以被忽略，有些實際問題，特別是那些要求連續進行適時預報的問題，常常希望依據實際上獲得的有限個數據x_t，x_t-1，…，x₁給出x_t+l的嚴格的線性最小方差預報，並希望隨t的增加，實現預報的適時遞推。新息預報方法就是滿足上述要求的一種預報方法。新息定理是新息預報的基礎。新息預報雖然公式較複雜，但占用的記憶體是有限的，並不隨t而增長，而且每步預報是用遞推計算，特別是MA序列，由新息預報公式可以看出，只要能判斷出MA模型的階數，不必計算出滑動平均參數就可以遞推進行新息預報。

由新息定理可以看出，時刻t的新息e_t是隨著樣本數據x_t的輸入經過遞推而得到的。

可以證明，無論是AR、MA或ARMA序列，當k充分大後，新息適時預報都與平穩預報漸近趨於一致。因此，在實際套用時，對於連續預報問題如果要求從較少的數據開始預報，並希望儘可能給出精確的預報值，那么，在開始一個階段，可以進行新息適時預報。而當k增加到一定數值以後，為了減少每步的計算量，可以改用矢量遞推法進行平穩預報，這樣兩種方法結合使用，既可提高預報精度，又可節省計算量。

實際進行新息預報時，計算過程是比較複雜的，對於有關的計算方法和技巧的深入討論，請參考相關文獻。