數據(data)是事實或觀察的結果,是對客觀事物的邏輯歸納,是用於表示客觀事物的未經加工的的原始素材。數據可以是連續的值,比如聲音、圖像,稱為模擬數據。也可以是離散的,如符號、文字,稱為數字數據。數據相關性是指數據之間存在某種關係,如正相關,負相關。
基本介紹
- 中文名:數據相關性
- 外文名:data dependency
- 學科:數據相關性
- 定義:數據之間存在某種關係
- 有關術語:數據
- 領域:數據分析
數據(data)是事實或觀察的結果,是對客觀事物的邏輯歸納,是用於表示客觀事物的未經加工的的原始素材。數據可以是連續的值,比如聲音、圖像,稱為模擬數據。也可以是離散的,如符號、文字,稱為數字數據。數據相關性是指數據之間存在某種關係,如正相關,負相關。
數據相關性可以時序分析、空間分析等方法進行分析。數據相關性分析也面對著高維數據、多變數數據、大規模數據、增長性數據及其可計算方面等挑戰。...
相關性分析是指對兩個或多個具備相關性的變數元素進行分析,從而衡量兩個變數因素的相關密切程度。相關性的元素之間需要存在一定的聯繫或者機率才可以進行相關性分析。...
關聯分析又稱關聯挖掘,就是在交易數據、關係數據或其他信息載體中,查找存在於項目集合或對象集合之間的頻繁模式、關聯、相關性或因果結構。或者說,關聯分析是發現交易...
相關關係是一種非確定性的關係,相關係數是研究變數之間線性相關程度的量。由於...需要指出的是,相關係數有一個明顯的缺點,即它接近於1的程度與數據組數n相關,...
《數據相關性理論及其在並行處理中的套用》是由范植華著作,科學出版社出版的可供計算機系統研製人員和計算機技術工作者閱讀的書籍。...
序列相關性,在計量經濟學中指對於不同的樣本值,隨機干擾之間不再是完全相互獨立的,而是存在某種相關性。又稱自相關(autocorrelation),是指總體回歸模型的隨機誤差項...
在統計學領域,有些人將數據分析劃分為描述性統計分析、探索性數據分析以及驗證性數據分析;其中,探索性數據分析側重於在數據之中發現新的特徵,而驗證性數據分析則...
在 統計學中, 以查爾斯·斯皮爾曼命名的斯皮爾曼等級相關係數,即spearman相關係數。經常用希臘字母ρ表示。 它是衡量兩個變數的依賴性的 非參數 指標。 它利用...
圖集 相關性準則--大數據時代的高效能之道圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:美僚雅4...
數據分析師 是數據師Datician['detɪʃən]的一種,指的是不同行業中,專門從事行業數據蒐集、整理、分析,並依據數據做出行業研究、評估和預測的專業人員。...
這就是一種關聯關係。它實際上是保證數據完整性的一種做法.關聯關係表填寫說明 編輯 關聯關係表需要填寫的信息包括:關聯方名稱,納稅人識別號,國家(地區),地址,和...
大數據時代大數據的精髓 大數據帶給我們的三個顛覆性觀念轉變:是全部數據,而不是隨機採樣;是大體方向,而不是精確制導;是相關關係,而不是因果關係。...
存儲在數據庫中的所有數據值均正確的狀態。如果數據庫中存儲有不正確的數據值,則該數據庫稱為已喪失數據完整性。...
因此,數據建模的過程中,涉及到的專業數據建模工作,與企業的利益和用戶的信息系統密切相關。從需求到實際的數據庫,有三種不同的類型。用於信息系統的數據模型作為一...
數據關聯處理,也可以稱做數據分析或數據關聯分析。關聯分析是一種簡單、實用的分析技術,就是發現存在於大量數據集中的關聯性或相關性,從而描述了一個事物中某些屬性...
數據挖掘 · 估計(Estimation) · 預測(Prediction) · 相關性分組或關聯規則(Affinity grouping or association rules) · 聚類(Clustering)點擊...
麥肯錫全球研究所給出的定義是:一種規模大到在獲取、存儲、管理、分析方面大大超出了傳統數據庫軟體工具能力範圍的數據集合,具有海量的數據規模、快速的數據流轉、...
雖然在大數據時代傳統的智慧型數據分析法已經不能適應當前的需求, 但是依然有一定的相似性, 相關理論和技術依然可以沿用, 幾種常見數據分析法: 第一種方法是決策樹...
數據有效性是對單元格或單元格區域輸入的數據從內容到數量上的限制。對於符合條件的數據,允許輸入;對於不符合條件的數據,則禁止輸入。這樣就可以依靠系統檢查數據的...
《列表數據分析》是2011年格致出版社出版的圖書,作者是(美)諾克。本書由三種討論互動表分析的小冊子組成,分別是《對數線性模型》、《流動表分析》和《關聯模型》...
在單層的關聯規則中,所有的變數都沒有考慮到現實的數據是具有多個不同的層次的;而在多層的關聯規則中,對數據的多層性已經進行了充分的考慮。例如:IBM台式機=>...
數據分析師是為了適應大數據時代要求,加強正規化、專業化、職業化的數據分析師人才隊伍建設,進一步提升我國數據分析師的職業素質和能力水平,經國家相關部委統一頒布...
《實驗數據分析(下冊)》介紹實驗和測量數據分析中涉及的機率和數理統計及相關的數學知識,內容包括機率論、經典數理統計、貝葉斯統計、蒙特卡羅方法、極小化方法和去...
《關聯數據:全球資訊網上的結構化數據》介紹了在全球資訊網上使用關聯數據的實用技巧,並通過複雜性逐步增加的示例,循序漸進地探討HTTP URI、RDF、SPARQL查詢語言等基本概念。...
同時也無法保證數據的準確性,常常管理人員得到的數據已經是滯後了一兩天的數據;而對於現場的不良產品信息及相關的產量數據,如何實現高效率、簡潔、實時的數據採集更是...
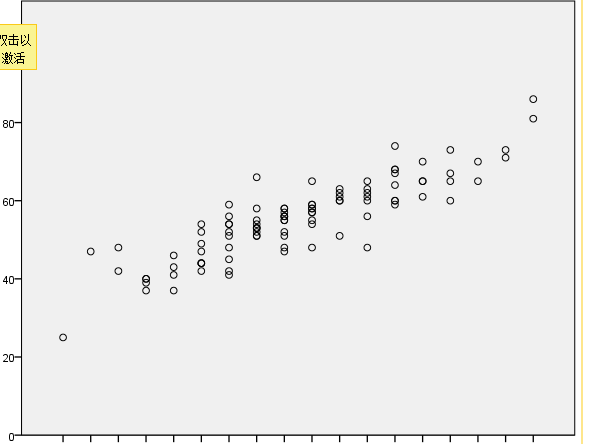
強相關又稱高度相關,即當一列變數變化時,與之相應的另一列變數增大(或減少)的可能性非常大。在坐標圖上則表現為散點圖較為集中在某條直線的周圍。...
