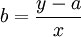散布圖法介紹
散布圖法由於將
全部成本數據均作為描述
成本習性的依據,其準確程度比
高低點法高。但因為其採用目測的方法得出固定成本,因而計算結果也具有一定的不準確性。
在質量管理過程中,經常需要對一些重要因素進行分析和控制這些因素大多錯綜複雜地交織在一起,它們既相互聯繫又相互制約既可能存在很強的相關性,也可能不存在相關性。如何對這些因素進行分析?散布團法便是這樣一種直觀而有效的好方法,通過做散布圖,因素之間繁雜的數據就變成了坐標圖上的點,其相關關係使一目了然地呈現出來。
在分析質量事故時,總是希望能夠尋找到造成質量事故的主要原因,但影響產品質量的因素往往很多,有時只需要分析具體兩個因索之間到底存在著什麼關係。這時可將這兩種因素有關的數據列出來,並用一系列點標在直角坐標繫上,製作成圖形,以觀察兩種因素之間的關係,這種圖就稱為散布圖,對它進行分析稱為
相關分析。
散布圖的分類
1、強正相關(如容量和附料重量)
2、強負相關(油的粘度與溫度)
3、弱正相關(身高和體重)
4、弱負相關(溫度與步伐)
5、不相關(氣壓與氣溫)
6、曲線相關
散布圖的構成
散布圖是由一直角坐標,其橫軸表示X變數的測定值,縱軸表示Y變數的測定值,將各組X測定值與Y測定值之交點全部繪出,即成為散布圖。
散布圖的特色
(1)從散布圖可簡單容易判斷X與Y兩個變數間:
·是否有相關關係。
·相關關係的強弱。
·是正相關或者負相關。
·是直線相關或是曲線相關。
(2)從散布圖上可簡單容易判斷數據是否有異常趨勢或是有沒有必要作層別分析。
散布圖的用途
(1)驗證兩個變數間的相關關係。
(2)掌握要因對特性的影響程度。
散布圖的作法
1、收集X與Y兩個變數足夠之對應數據。
2、計算X變數測定值的平均值,計算Y變數測定值的平均值。
3、在直角橫坐標X軸上劃出X值的刻度(刻度在軸的內側,數字標示在軸的外側),並且以最小值當起點,刻度間表示均為同等值。縱坐標Y軸上劃出Y值的刻度(刻度在軸的內側,數字標示在軸的外側),並且以最小值當起點,刻度間表示均為同等值。
4、X軸與Y軸之交點處不可標示0數字,並且X軸的全寬度與Y軸的全寬度最好相等。
5、將各組之數據的點繪於坐標上:
(1)如有2點重複時以⊙表示。
(2)如有3點重複時以⊙表示。
應注意事項
1、兩組變數的對應數至少在30個以上,最好50個,100個最佳。
2、找出X、Y軸的最大值與最小值,並以X、Y的最大值及最小值建立X-Y坐標。
3、通常橫坐標用來表示原因或自變數,縱坐標表示效果或因變數。
4、散布圖繪製後,分析散布圖應謹慎,因為散布圖是用來理解一個變數與另一個變數之間可能存在的關係,這種關係需要進一步的分析,最好作進一步的調查。
散布圖法步驟
散布圖法的工作步驟為:
1)收集歷史數據
將各期總成本數據標入直角坐標系,畫出散布圖。
3)確定固定成本平均值
根據離散的歷史成本點目測成本隨產量變動的趨勢,畫出一條能反映成本平均變動趨勢的直線,直線與縱軸的交點即固定成本平均值。
4)計算單位變動成本
在直線上任取一點,根據
的計算公式,計算出單位變動成本。
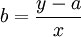
5)計算總成本
按照計算出的固定成本平均值(a)、單位變動成本(b),預測未來某期產量下的總成本,預測公式為:
y = a + bx
式中:y—未來預測期的總成本;x—產量。
散布圖法示例
例如:某公司2007年1~6月份,某項
混合成本與有關產量的歷史資料如表所示,採用散布圖法進行成本習性分析。
月份
| 產量(件)
| 成本(元)
|
1
| 30
| 340
|
2
| 20
| 250
|
3
| 52
| 560
|
4
| 35
| 380
|
5
| 40
| 430
|
6
| 25
| 280
|
1.首先,將2007年1~6月份的產量和成本的坐標點分別標註在坐標圖上。
2.其次,目測一條能夠反映成本變動趨勢的直線,直線與縱軸的交點為固定成本,在圖中讀出該直線的截距為a=75;
3.在直線上任取一點,測出坐標為(20,250),計算b值為:
(元/件)

4.代入a,b值,得出成本習性模型為:y = 75 + 8.75x