擾率

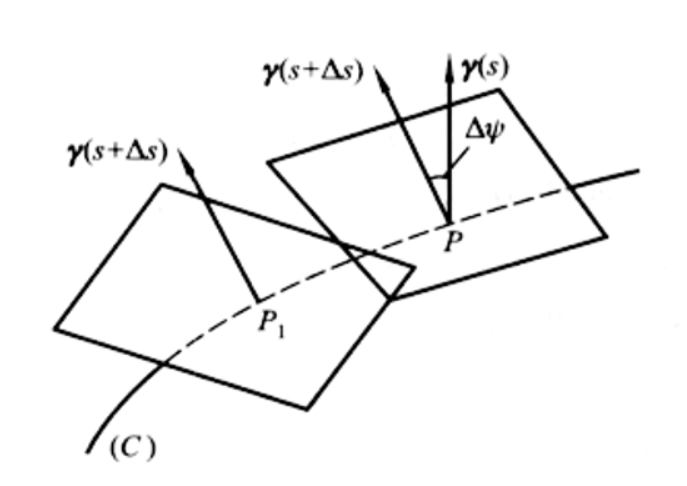
擾率是研究刻畫空間曲線在某點臨近離開平面的程度的量，它是反映空間曲線扭曲程度的一個重要的幾何量，又被稱之為曲線的第二曲率。

基本介紹

• 中文名：擾率
• 外文名：Torsion
• 意義：反映空間曲線的扭曲程度
• 性質：擾率絕對值越大，扭曲程度越大
• 解釋：副法向量的轉動速度

定義

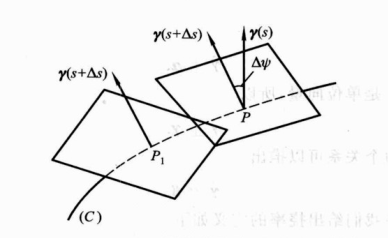
當曲線扭轉時，副法向量（或密切平面）的位置隨之改變，所以我們用副法向量（或密切平面）的轉動速度來刻畫曲線的扭轉程度。擾率即刻畫扭轉程度的量。

1、曲線在一點的擾率定義為

為空間曲線的副法向量和主法向量。

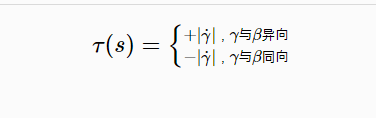
2、擾率絕對值定義式

ΔΨ表示兩個副法向量的夾角。

擾率的絕對值度量了曲面上臨近兩點的副法向量的夾角對弧長的旋轉速度，當曲線在一點的扭轉程度越大，副法向量（或密切平面）對於弧長的旋轉速度就越大。

計算公式

1、一般參數的擾率計算公式

給定 類空間曲線C

擾率的計算公式為

2、自然參數的擾率計算公式

給定 類空間曲線C

擾率的計算公式為

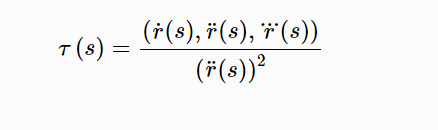
3、曲率和擾率的關係式

曲率刻畫曲線的彎曲程度，而擾率刻畫曲線的扭轉程度。則一般曲線的曲率和擾率之間的關係為：

給定 類空間曲線C

它的曲率和擾率分別為 ，則一定存在關於t的函式 ,使曲率和擾率成立如下的關係式：

計算實例

例：求圓柱螺線 的擾率

解：

於是有，

由以上可以看出，圓柱螺線的擾率為常數。

性質及意義

1、對於空間曲線，曲線不僅彎曲而且還要扭轉（離開密切平面），所以研究空間曲線只有曲率的概念是不夠的，還要有刻畫曲線扭轉的程度的量——擾率。我們用副法向量的轉動速度來刻畫曲線的扭轉程度。

2、當擾率非0時，稱其倒數為擾率半徑。

3、當擾率 時，該空間曲線為平面曲線。反之，平面曲線的擾率恆等於零。

4、我們稱擾率不恆為零的曲線為擾曲線。

5、擾率關於剛性運動的不變性。是指當曲線C經過 中的一個運功變為C'，C和C'上對應的擾率相等。

6、擾率關於參數變換的不變性。表明曲線在容許的參數變化下，對應點的擾率不變，即擾率為參數變換下的不變數。