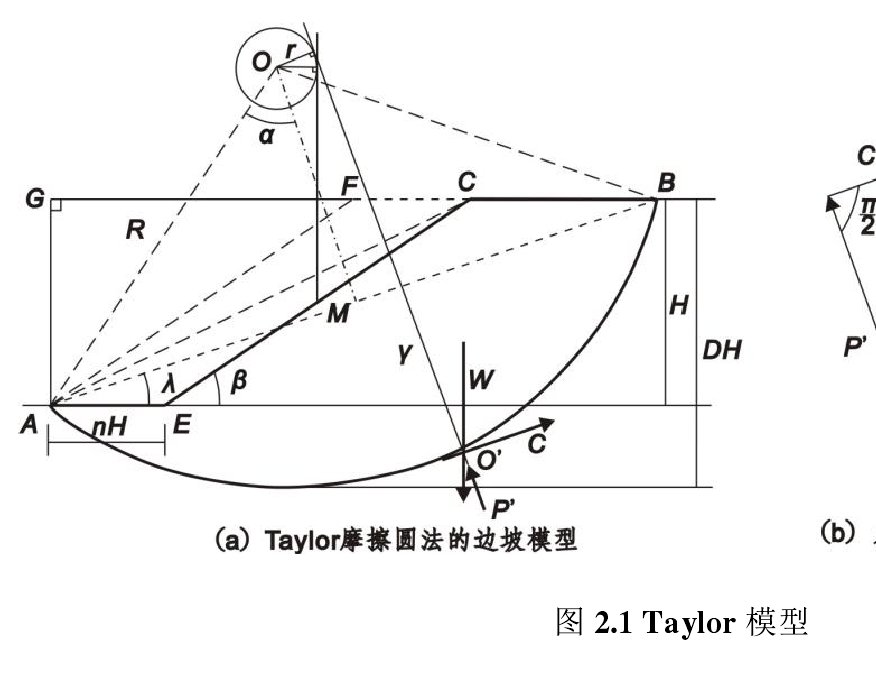
摩擦圓法是經典土坡穩定性計算方法之一,該方法限於均質簡單土坡,只有2條假定,一是假定滑動面為圓弧,二是假定整個底滑動面上摩擦力和正應力的合力與摩擦圓相切。摩擦圓與滑動面圓弧同心,半徑為滑動面圓弧半徑R與內摩擦角φ正弦的積,即Rsin(φ),故稱摩擦圓法。
基本介紹
- 中文名:摩擦圓法
- 外文名:friction circle method
- 學科:土木工程
- 提出者:泰勒
- 套用:土坡穩定計算
- 假設:合力與摩擦圓相切
簡介,研究現狀,有關術語,
簡介
摩擦圓法是由 Glennon Gilboy 和 Authur Casagrande 最早提出的,起初是一種解決邊坡問題的完全圖解法。Taylor, D.W.(1937)提出了“穩定數”的概念,導出了穩定數的解析解公式。穩定數是將平衡公式中的粘聚力、穩定係數、重度和坡高單獨提取出來構成的獨立項。Taylor的穩定數表達式簡單、直觀,可方便地用圖表表示。Taylor摩擦圓法適用於均質簡單土坡,即粘聚力c、內摩擦角φ的值是常數。該方法不同於條分法,可做整體分析,因此無需對條間力作任何假定,同時滿足力和力矩平衡,有嚴密的數學推導和解析表達,是極限平衡法中較為嚴謹的一種方法。摩擦圓法平衡公式中的黏聚力、重度和坡高均為線性項,可單獨提取出來,並將穩定係數定義為對黏聚力的折減係數,由此構成一個獨立項,即穩定數。
研究現狀
Taylor 摩擦圓法針對均質簡單土坡,其剪下強度參數c和 φ 是常數。Gibson, R.E.,Morgenstern, N.(1962)和 Hunter, J.H.(1968)以飽和不排水的粘性土坡(φ=0)為研究對象,假定其粘聚力 c 呈線性增長趨勢,基於 Taylor 摩擦圓法,推導出其穩定數表達式,並編繪成圖表。由於 Taylor 穩定數圖表中沒有考慮穩定係數對內摩擦角的折減,在實際套用時需通過類似於疊代的過程反覆查穩定數圖表來確定邊坡的穩定係數。為此 Baker, R.和 Tnaka,Y.(1999)對 Taylor 摩擦圓法做了一些改進,引入無量綱參數 λ,表示穩定數同時對粘聚力和內摩擦角進行了折減。利用該參數,重新繪製穩定數圖表,避免了求解穩定係數過程中的反覆疊代。Taylor 摩擦圓法是根據大量試算得到邊坡的最大穩定數,此時邊坡處於臨界滑動狀態,文章中僅列舉了部分臨界滑動面的位置參數。針對臨界滑動面位置的確定問題,Baker, R.(2003)將滑坡形態劃分為三類,並以圖表的形式展示不同邊坡條件時的臨界滑動面類型,方便直接查圖表確定穩定係數及相應臨界滑動面的位置。
有關術語
內摩擦角
在以土的抗剪強度為縱坐標、剪下破壞面上的 法向應力為橫坐標的坐標系中,土的抗剪強度包線 對橫坐標軸的傾角。 通常以φ表示, 是土的抗剪 強度參數之一,其值與土的初始孔隙比、土粒形狀、土的顆粒級配和土粒表面的粗糙度等因素有關。可由土的直接剪下試驗或三軸壓縮試驗測定, 根據不同的試驗方法和分析方法可得出總應力內摩 擦角和有效應力內摩擦角。
粘聚力
粘聚力,又叫內聚力,是在同種物質內部相鄰各部分之間的相互吸引力,這種相互吸引力是同種物質分子之間存在分子力的表現。在有效應力情況下,將總抗剪強度扣除摩擦強度,即得到粘聚力。從另一角度看,粘聚力是破壞面沒有任何正應力作用下的抗剪強度。
土坡穩定分析
在土木工程建築中,如果土坡失去穩定造成塌方,不僅影響工程進度,有時還會危及人的生命安全,造成工程失事和巨大的經濟損失。因此,土坡穩定問題在工程設計和施工中應引起足夠的重視。天然的斜坡、填築的堤壩以及基坑放坡開挖等問題,都要演算斜坡的穩定性,亦既比較可能滑動面上的剪應力與抗剪強度。這種工作稱為穩定性分析。土坡穩定性分析是土力學中重要的穩定分析問題。土坡失穩的類型比較複雜,大多是土體的塑性破壞。而土體塑性破壞的分析方法有極限平衡法、極限分析法和有限元法等。在邊坡穩定性分析中,極限分析法和有限元法都還不夠成熟。因此,工程實踐中基本上都是採用極限平衡法。極限平衡方法分析的一般步驟是:假定斜坡破壞是沿著土體內某一確定的滑裂面滑動,根據滑裂土體的靜力平衡條件和莫爾—庫倫強度理論,可以計算出沿該滑裂面滑動的可能性,即土坡穩定安全係數的大小或破壞機率的高低,然後,再系統地選取許多個可能的滑動面,用同樣的方法計算其穩定安全係數或破壞機率。穩定安全係數最低或者破壞機率最高的滑動面就是可能性最大的滑動面