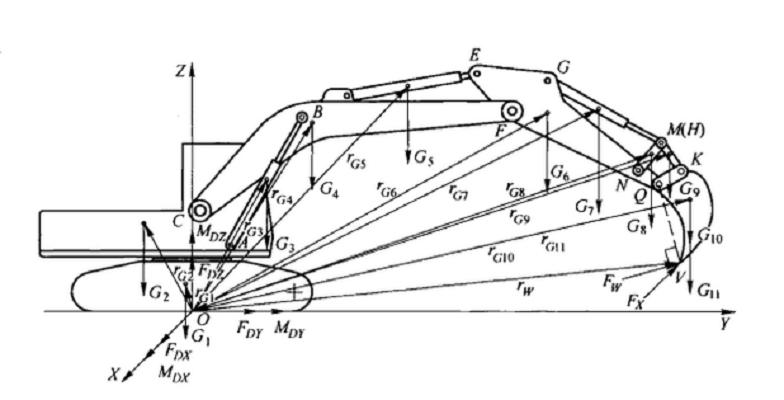
概念
物體和地面接觸的單位面積上所承受的垂直載荷,稱為接地比壓。研究接地比壓是研究物體-地面附著力矩的重要基礎。研究接地比壓能夠解釋接地比壓隨物體中心變化而變化的規律,和比壓和深陷程度的關係等等。故理解和認知接地比壓對我們研究機械行駛問題有著重要幫助。
履帶接地比壓
履帶單位接地面積所承受的垂直荷載,稱為履帶接地比壓。這是履帶式工程機械的一個非常重要的技術參數,它直接決定機器的行駛通過性和工作穩定性,也是研究履帶一地面附著
力矩的先決條件。
對於具有兩條履帶的工程機械來說,當工作重力與垂直外載荷所構成的合力在水平地面上的投影同履帶接地區段的幾何中心相重合時,履帶接地比壓便呈
均勻分布狀態,稱為
平均比壓,其表達式為:
式中:
——履帶平均接地比壓,
;
——機器工作重力與垂直外載荷所構成的合力,
;
--履帶接地寬度,
;
--履帶接地區段長度,
。
當機器重心在水平地面上的投影與履帶接地區段的幾何中心相重合,且履帶接地區段面積和地面都很光滑並近似於水平狀態時,按上式計算的結果與實際情況非常接近。平均接地比壓是履帶機器的一個重要指標,在機器的使用說明書中一般都要註明。
設計履帶式工程機械時,在總體布置上要儘量使垂直載荷對稱並均勻地作用於履帶接地區段上,這是保證履帶機器具有良好的行駛通過性和工作穩定性的必要條件。
但是,平均接地比壓並不代表機器的實際接地比壓,因為機器重心在水平地面上的投影,一般不會恰好與履帶接地區段的幾何中心相重合。因此必須研究機器的最大接地比壓和最小接地比壓;最大接地比壓才能反映機器的實際行駛通過性和工作穩定性。
假設履帶行駛裝置兩條履帶接地區段的幾何中心為O點,通過該點引出相互垂直的縱向與橫向中心線x和y。這樣便形成一個直角坐標系(圖1)。在一般情況下,重心的投影總是落在該直角坐標系的某個象限內(圖1表示在第一象限)。C為機器橫向偏心距,e為機器縱向偏心距。
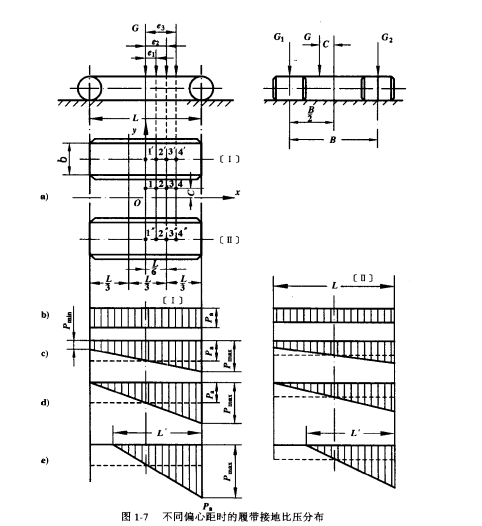 圖1
圖1由於橫向偏心距C的影響,機器重力與垂直外載荷所構成的合力,對兩條履帶的作用不是平均的。假設履帶Ⅰ所承受的重力為
,履帶II所承受的重力為
,則根據圖1可列出以下方程式:
由此得兩條履帶所承受的不同載荷的計算式為:
根據式上兩式可知,由於機器存在橫向偏心距C的原因,距重心較近的履帶Ⅰ所承受的載荷G,較大,因而機器的最大接地比壓必然發生在履帶I的下部;履帶Ⅱ的接地比壓分布形式與履帶I相同,但相應的數值較小,當
時,則
,即機器重心的投影恰好落在履帶接地區段的縱向中心線x軸上。此時兩條履帶的接地比壓分布形式及數值完全相同。
當機器重心位於履帶接地區段橫向y軸上的點1時,即橫向偏心距為C,縱向偏心距為零,則兩條履帶的接地比壓都呈均勻分布狀態,壓力圖為矩形(圖1b)。
履帶Ⅰ的平均接地比壓為:
同理:
當機器重心在履帶裝置幾何中心左右變化,且變化範圍為e=0~L/6時(如圖1a)上點2),則接地比壓圖形為梯形[圖1c)]。在此情況下,履帶I的最大和最小接地比壓為:
式中:
——履帶接地平面模量,
。
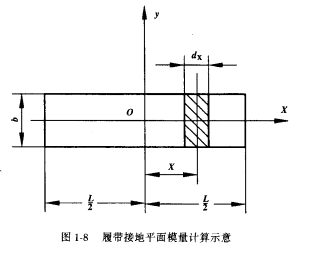 圖2
圖2綜合上述得:
在此情況下,履帶I接地區段任意部位接地比壓的計算式,可以通過上式以及圖3所示的相關幾何關係求出。
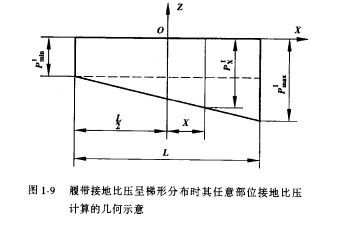 圖3
圖3船體的接地比壓
當機耕船靜置於水田中時(圖4),其垂直方向的受力平衡方程式為:
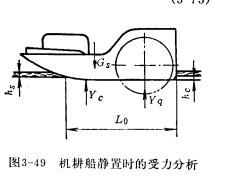 圖4
圖4——船體的接地面積,為船體在陷深
時的接地長度
和接地寬度
的乘積;
分析上式中的各項:
①
為水的浮力。當
=3~8厘米(平均5厘米)時,可近似看作
公斤/厘米
2。
② 土壤對船體的垂直反力
,同船體的接地面積
、以及土壤在陷深
處的抗壓強度
有關,可以近似認為
③ 土壤對驅動輪的反力
,隨驅動輪的入土深度,該深度處土壤的機械強度,以及驅動輪的形狀和參數的不同而有很大差別。據湖北-12型機耕船的電測試驗結果,在泥腳深超過30厘米的水田中靜止和帶負荷直行時,驅動輪反力
分別占整機重量的34.9%o和46.1%(平均值)。
④在計算機耕船的最大接地比壓時,考慮到惡劣的使用條件——無水或少水,土壤極稀軟、驅動輪嚴重滑轉等情況,可不計水的浮力和驅動輪的支反力,即假設:
若機耕船的
平均接地比壓為
,在上述假設條件下,它和整機使用重量
的關係式應為:
綜合上面公式,可得到機耕船在上述假設條件下靜置而不下陷的平衡條件:
式中
——許用比壓值,即是土壤在船底陷深處的抗壓強度
。
的數值由所設計機耕船的規定限深和該機使用地區的土壤承壓特性曲線來決定。當
=3~5厘米時,根據各類土壤抗壓強度的統計數據,可取如下數值:









 圖1
圖1

















 圖2
圖2


 圖3
圖3



 圖4
圖4