拼方(squaring the square)是一種組合構形,指將若干個邊長互不相等的正方形拼成一個正方形,換句話說,將一個正方形剖分為若干個小正方形使得它們的邊長互不相同。
基本介紹
- 中文名:拼方
- 外文名:squaring the square
- 所屬學科:數學
- 所屬問題:組合學(圖與超圖)
基本介紹,完美正方形,
基本介紹
拼方是將若干個邊長互不相等的正方形拼成一個正方形,換句話說,將一個正方形剖分為若干個小正方形使得它們的邊長互不相同,這樣的正方形稱為完美正方形。找完美正方形的過程稱為拼方,魯金(Н.Н.Лузин)曾猜想沒有這樣的正方形.第一個完美正方形是德國的斯普拉格(R.Sprague)於1939年發現的,同時,英國劍橋大學的四名學生布魯克斯(R.L.Brooks)、史密斯(C.A.B.Smith)、斯通(A.H.Stone)和塔特(W.T.Tutte)於1940年發現了一種基於電網路的組合理論行之有效的拼方的方法。他們首先研究將長方形剖分為邊長互不相等的正方形,這種長方形稱為完美矩形。進而,他們還研究了將等邊三角形剖分為面積互不相等的等邊三角形,稱這種三角形為完美三角形。他們的方法對圖論中的連通度的理論、著色理論、網路流的理論、圖的平面性與對偶性、圖的曲面嵌入,以及圖的對稱性和定向等都產生了重要的影響.一個完美正方形是簡單的,是指它不能分割成至少兩個完美矩形。完美正方形的階是指組成完美正方形的小正方形的數。杜尤斯蒂因(A.J.W.Duijuestijn)於1978年發現了惟一的一個階為21的簡單完美正方形,這是階最小的簡單完美正方形,圖給出了此完美正方形,其中的數字表示所在正方形的邊長。
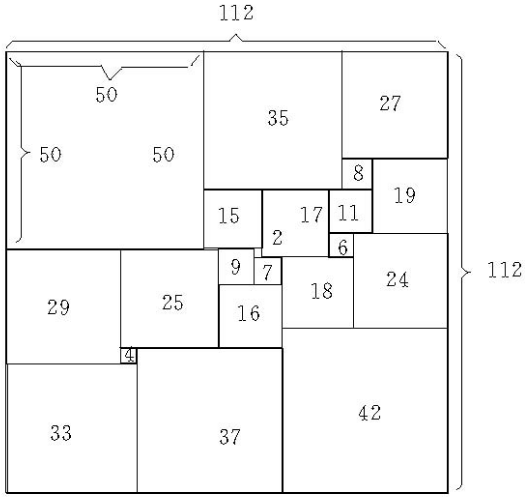 圖1
圖1完美正方形
我們能不能將一個大正方形分割為一些彼此互不相同的小正方形?或者反過來說,我們能不能用一些大小各不相同的小正方形拼合成一個大正方形?這樣的一個大正方形,叫做完美正方形 (又稱完全正方形)。
第一個完美正方形是由英國劍橋大學的四位數學家組成的研究小組於1938年發現的, 可分為69個小正方形,因此稱為69階完美正方形。此後,又有許多其他階的完美正方形被發現。於是,人們試圖尋找一個由個數最少的小正方形拼合而成的(即最低階的)完美正方形。
利用電子計算機已經證明: 不存在20階或20階以下的完美正方形。1978年,荷蘭數學家A. J. W.杜伊傑斯廷(Duijvestijn)發現了21階的完美正方形,邊長為112,如圖 (圖中數字為小正方形邊長)。更加奇妙的是,它還是一個簡單完美正方形,即其中的小正方形不構成任何矩形。杜伊傑斯廷的發現很可能是獨一無二的,也就是說,很可能再也沒有與此不同的21階完美正方形了。
既然我們能用邊長互不相同的一些小正方形拼合成一個大正方形,那么,能不能用邊長分別為1,2,3,4,……(即相繼的自然數)的正方形去鋪滿整個平面?在這裡請注意:平面是可以在各個方向任意延伸的,自然數的個數是無窮的。我們的問題要求:對每一個自然數,恰好有一個相應邊長的正方形被鋪在平面上;平面上的任何一個區域都要被這些正方形覆蓋住, 任何兩個正方形之間既不能互相重疊, 也不能留下空隙。
自從完美正方形被人們發現之後, 這個問題就被注意到了,但至今仍未能獲得解決。利用著名的斐波那契(Fibonacci)數列的性質,已經證明用這樣的正方形至少可以鋪平面的四分之三。也就是說,任取平面上一塊足夠大的區域, 則其中沒有被蓋住的部分面積之和不會超過四分之一。當然,這離問題的徹底解決可能還是相當遙遠的。

