拋球問題

拋球問題(the problem of toss a ball)一種矛盾命題，指西方數理哲學界流傳甚久而未解決的一個問題，即芝諾悖論的引申。

基本介紹

• 中文名：拋球問題
• 外文名：the problem of toss a ball

理論提出

由於近代極限論和無窮級數理論的誕生，人們可按收斂無窮級數得以求和的觀點，對古代著名的芝諾悖論給出邏輯、數學的解釋方法.並隨之將芝諾悖論引申為下述拋球問題:設有甲、乙二人互相拋球，甲先用1/2分鐘把球拋給乙，乙又用1/4分鐘時間把球拋回甲手中，然後甲又用1/8分鐘時間把球拋給乙……如此往復以至無窮.那么根據收斂無窮級數求和法則，可對甲、乙二人所費拋球時間求和，即

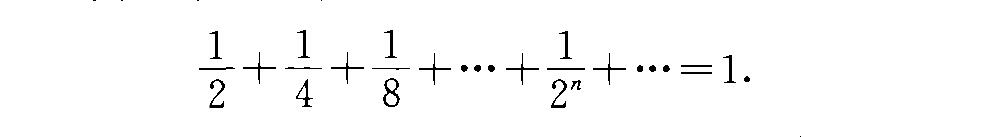
理論推想

試問:當拋球自開始進行到1分鐘時，該球落在甲手中，還是落在乙的手中?這就是所謂拋球問題.對此，由於潛無限論者不承認任何無窮過程得以進行完畢，因而上述拋球將永遠只能滯留於無限制的往復進程中，從而可以避而不答這個問題.但實無限論者卻既不能迴避問題，又無法回答這個問題.故亦有拋球悖論之稱，並在西方數理哲學界流傳一時，久久未決.

論證研究

徐利治、朱梧櫻等人於1982年利用奧斯道爾- 高橋(Osdos-Takahashi)關於超冪`R這個實數的非標準模型，引進潛變段(即潛尾)存在公理，建立了非康托爾型自然數序列模型，進而利用這一非康托爾型自然數序列模型N的構造特徵，對拋球問題給出了一種邏輯、數學的解釋方法.亦即將拋球時間序列 { t,)放到‘R上來考察，於是可將{t}}與{(n)}對應起

今在N的潛變段中選取無窮多個偶的無限自然數與奇的無限自然數:

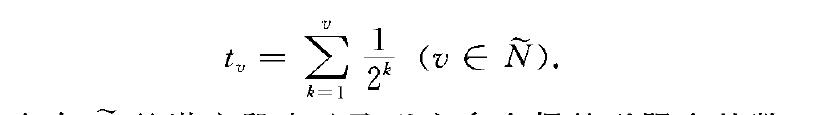
此處j=1,2,…於是在這些時刻氣和氣，可認為球仍將分別落到A處和B處.但因。與竹，產，等皆為無限自然數，故廣義實數t二的標準部分為

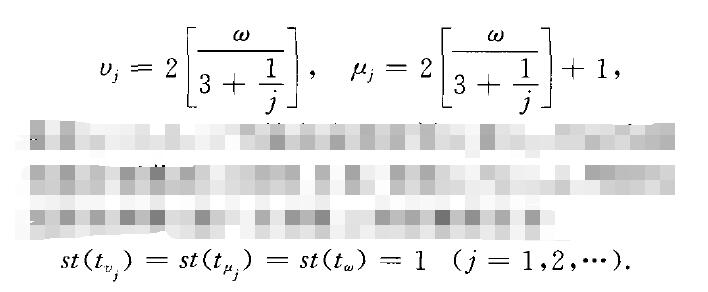
這表明拋球時間達到1分鐘時，該球抵達甲手中和乙手中各有無窮多次(當然，球在甲、乙之間任一位置也有無窮多次). 如上解釋的結論看似乎很怪，但只要想到時點如同非標準數軸上的實數點那樣，它是具有內部結構的，那就不足為怪.實際上此處正是利用了非標準實數(如t}，與t}k)的這種能夠無限多地凝聚在標準實數(如Il之無限小鄰域的特點.。