基本介紹
剛性

平面度
稀疏度


構造

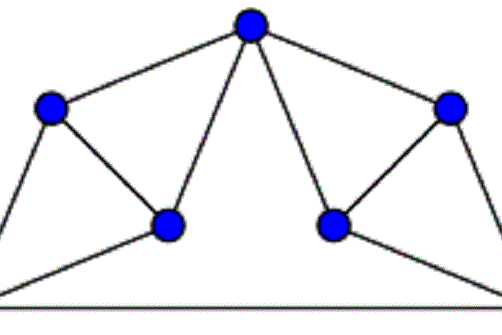




在圖論中,拉曼圖是一類稀疏圖,描述了平面中桿和接頭的最小剛度系統。 形式上,拉曼圖是在n個頂點上的圖,這樣,對於所有k個圖,每個k個頂點子圖最多具有2k-3個邊,而整個圖恰好具有2n-3個邊。 拉曼圖以阿姆斯特丹大學的傑...
《礦物的標準拉曼圖譜庫及檢索系統》是由地質礦產部礦床地質研究所、清華大學分析中心擔任第一完成單位,由王阿蓮、韓景儀、郭立鶴、郁鑒源、曾佩擔任主要完成人的科研項目。成果信息 成果摘要 根據對礦物晶體全對稱的拉曼活性振動模式的分析...
共振拉曼光譜學與其他分子光譜學一樣,是闡明原子、分子、離子以及結晶體系的工具。其特長是研究自由的或弱相互作用下的分子和多核離子的結構。(1)利用共振拉曼光譜圖上的泛音頻率測定光譜常數。以往只有在簡單分子的氣體紅外光譜中能觀察到...
拉曼光譜(Raman spectra),是一種散射光譜。拉曼光譜分析法是基於印度科學家C.V.拉曼(Raman)所發現的拉曼散射效應,對與入射光頻率不同的散射光譜進行分析以得到分子振動、轉動方面信息,並套用於分子結構研究的一種分析方法。現象介紹...
拉曼效應(Raman scattering),也稱拉曼散射,1928年由印度物理學家拉曼發現,指光波在被散射後頻率發生變化的現象。1930年諾貝爾物理學獎授予當時正在印度加爾各答大學工作的拉曼(Sir Chandrasekhara Venkata Raman,1888——1970),以表彰他...
顯微拉曼圖像光譜分析儀是一種用於化學工程領域的分析儀器,於2012年6月25日啟用。技術指標 拉曼頻移範圍:532nm激發100-8000/cm,632nm激發100-5500/cm,785nm激發100-3200/cm。主要功能 用於拉曼光譜技術套用研究方法和平台比對校準,及...
拉曼光譜分析法是基於印度科學家C.V.拉曼(Raman)所發現的拉曼散射效應,對與入射光頻率不同的散射光譜進行分析以得到分子振動、轉動方面信息,並套用於分子結構研究的一種分析方法。拉曼光譜(Raman spectra),是一種散射光譜。當光穿過...
拉曼光譜和紅外光譜一樣同屬於分子振動光譜,可以反映分子的特徵結構。但是拉曼散射效應是個非常弱的過程,一般其光強僅約為入射光強的 10^-10。所以拉曼信號都很弱,要對表面吸附物種進行拉曼光譜研究幾乎都要利用某種增強效應。Fleischmann...
A·R·拉曼全名Allah Rakkhha Rahman(泰米爾文:அல்லா ரக்கா ரஹ்மான்,1966年1月6日-),簡稱A. R. Rahman,出生於印度,他身兼作曲、唱片監製及音樂人於一身,被稱為當今世上...
傅立葉變換拉曼光譜可測定含螢光和對光不穩定的化合物的拉曼光譜,進行化合物的全譜掃描,且速度快,譜圖重現性好。近全外光激發,可直接測到生物組織內分子的信息。在化學、生物和生物醫學樣品的非破壞性結構分析方面具有優勢,可望...
b. 在以波數為變數的拉曼光譜圖上,斯托克斯線和反斯托克斯線對稱地分布在瑞利散射線兩側, 這是由於在上述兩種情況下分別相應於得到或失去了一個振動量子的能量。c. 一般情況下,斯托克斯線比反斯托克斯線的強度大。這是由於Boltzmann分布...
拉曼光譜法是研究化合物分子受光照射後所產生的散射,散射光與入射光能級差和化合物振動頻率、轉動頻率的關係的分析方法。 與紅外光譜類似,拉曼光譜是一種振動光譜技術。所不同的是,前者與分子振動時偶極矩變化相關,而拉曼效應則是分子...
近場拉曼光譜具有如下優點:(1) SNOM 帶來更高的空間解析度以及較低的背景散射 (瑞利散射減小),使得獲取高於遠場光譜理論極限的納米空間尺寸的局域拉曼光譜成為可能;(2) 可以在獲得樣品的拉曼譜的同時得到近場形貌圖,兩者結合更易於對...
《拉曼譜學——峰強中的信息》是2013年科學出版社出版的圖書,作者是吳國禎。內容簡介 本書的核心思想是從拉曼峰強的角度,來理解拉曼譜圖背後的物理、化學過程和圖像。主要介紹作者所創立的從拉曼峰強求取鍵極化率的思路和方法。本書...
生命科學聯合中心陳興研究組與北京大學生物動態光學成像中心黃岩誼研究組合作,開發了一種全新的活細胞成像技術:生物正交標記受激拉曼散射顯微術。它是基於單一化學鍵標記的受激拉曼散射顯微術,突破了成像標記基團的尺寸極限。研究者 北京...
是一種檢測新冠病毒的技術。介紹 “新冠病毒及其變異株拉曼光譜快速檢測技術”使用僅有手機大小的手持式拉曼光譜儀,即可在5分鐘內快速、靈敏地檢測出新冠病毒及其變體,自動化儀器一代已經完成,二代儀器目前正在調試中。
色散拉曼-付變拉曼及共聚焦顯微聯用系統是一種用於生物學、化學、能源科學技術領域的分析儀器,於2012年10月30日啟用。技術指標 雷射器配有3種不同激發波長,分別為532nm、785nm、1064nm;掃描範圍:50-4475cm-1。配有雷射共聚焦組件...
全球最小的掌上拉曼光譜儀 DeltaNu研製出了全球最小的掌上拉曼光譜儀ReporteR——其體積僅為手機大小,可獨立工作,也可用USB連線電腦做實時譜圖分析。台式拉曼光譜儀 Advantage 532是一台低價高性能的台式拉曼光譜儀。相對於Advantage系列...
共聚焦拉曼顯微鏡是一種用於電子與通信技術領域的儀器,於2014年12月05日啟用。技術指標 激發波長:488,532,785 nm;光柵:300, 600,1800 G/mm; 光譜解析度:1 cm-1; 空間解析度:200 nm; 線掃描範圍:120 um @ 50x物鏡。...
顯微雷射拉曼是一種用於材料科學、環境科學技術及資源科學技術領域的分析儀器,於2013年12月23日啟用。技術指標 空間解析度為橫向1µm,縱向2µm;最低波數10cm-1;光譜重複性≤±0.03cm-1;光譜範圍50-9000cm-1;光譜解析度≤0...
拉曼-原子力顯微鏡連用成像分析系統是一種用於生物學、藥學、化學、能源科學技術領域的分析儀器,於2016年12月14日啟用。技術指標 配備了532nm和785nm的雷射光源,拉曼光譜儀解析度≤ 0.8 cm-1,高靈敏CCD檢測器,拉曼共聚焦模式成像...
拉曼光譜系統是一種用於物理學、化學、生物學、材料科學領域的分析儀器,於2009年05月26日啟用。技術指標 1.光源:514nm,633nm;785nm2.頻率範圍:150-6000cm-13.光譜範圍:200-1600nm4.樣品狀態:固態或液態5.光柵:1800gr/mm...
