抖動積累（jitter accumulation）是指將若干數字通信設備級聯時，各設備所接收的抖動與其自身的抖動相加的過程。實際中，由於定時電路的不完善，傳輸中信號受噪聲的干擾，接收端提取出來的定時信號呈現隨時間不規則的晃動，即定時抖動。定時抖動使再生判決瞬間發生偏差，這不但使判決瞬間的信噪比惡化，而且還會反映到再生後的信號中，使再生後的信號產生相位調製，傳到下一個中繼器，形成抖動積累。
| 中文名稱 | 抖動積累 |
| 英文名稱 | jitter accumulation |
| 定 義 | 將若干數字通信設備級聯時，各設備所接收的抖動與其自身的抖動相加的過程。 |
| 套用學科 | 通信科技（一級學科），通信原理與基本技術（二級學科） |
基本介紹
- 中文名：抖動積累
- 外文名：jitter accumulation
簡介,抖動源,隨機性抖動源,系統性抖動源,理論模型,隨機性抖動的積累,系統性抖動的積累,抖動積累的特點,隨機性抖動的影響不容忽視,碼型相關抖動不一定按系統牲抖動積累,數欄位內總的抖動積累效應有所減弱,
簡介
定時抖動的積累是多中繼數字傳輸系統中極為重要的問題。再生中繼器的定時信號，通常採用直接從信號碼流中提取的自定時方式。實際中，由於定時電路的不完善，傳輸中信號受噪聲的干擾，接收端提取出來的定時信號呈現隨時間不規則的晃動，即定時抖動。定時抖動使再生判決瞬間發生偏差，這不但使判決瞬間的信噪比惡化，而且還會反映到再生後的信號中，使再生後的信號產生相位調製，傳到下一個中繼器，形成抖動積累（jitter accumulation）。
關於電纜傳輸的抖動性能研究已比較完善。抖動分為與信號隨機性有關的圖案噪聲和與信號無關的熱噪聲。但是，在光纖通信中，除了以上兩個抖動源外，還存在第三個抖動源--散彈噪聲。散彈噪聲的統計特性與前兩種噪聲完成不同，且當採用雪崩光電二極體(APD)作光電檢測器時，它是起主要作用約噪聲源。
電纜中傳輸信號通常採用正負交替的脈衝序列，其頻譜中沒有1/T處的譜線，必須將信號進行非線性處理，才能定時提取。在光纖通信中，則常採用單極性歸零碼，這時的信號序列含有傳輸速率1/T處的譜線，故可直接提取定時信號，而不需要作預處理。通常把沒有預處理的定時電路稱作簡單定時電路。文獻利用定時抖動功率譜密度的統一範式，詳細分析i割辰槽路(RC)式定時電路的抖動功率譜密度分布及抖動積累特性，給出抖動積累方差的簡化公式。這些簡化公式在工程估算中是十分方便的。
抖動源
隨機性抖動源
- 各種噪聲源：在光纜系統中，除了一般電纜系統所具有的熱噪聲外，接收機的雪崩二極體還會產生可觀的雪崩噪聲。雷射器本身會產生量子噪聲、紐結噪聲、模分配噪聲及反射噪聲。雷射器與很短的光纖段相結合還會產生模式噪聲。這些噪聲的機理不盡相同，但其結果都會使信號脈衝波形發生隨機畸變，從而使定時濾波器的輸出信號波形產生隨機的相位寄生調製，形成抖動。
- 雷射器的跳模和光反饋：由於溫度和其他條件的影響，雷射器的工作模式會發生隨機跳動，使傳輸信號的延遲發生變化，導致定時判決點偏離最佳時刻，形成抖動。這種雷射器的跳模現象，如果與光源側的不完善接頭所造成的光反饋相結合，甚至會造成定時信息的暫時消失。但是，這種隨機跳模所造成的影響是暫時的，不會形成恆定的損傷，而且在系統設計中可以設法儘量避免。
- ③定時濾波器失諧：定時濾波器的有效品質因數總是有限的，因而傳輸信息中靠近時鐘頻率的一小段連續譜也會得到輸出。當濾波器失諧時，將產生不對稱的輸出波形，等效於非對稱邊帶的調製，造成時鐘分量幅度和相位上的調製。其中相位調製將弓!起定時抖動。
- 完全不相關的碼型抖動：在碼型相關抖動中有一部分是完全不相關的抖動，其積累特性如同隨機噪聲一樣，可以按隨機性抖動處理。
系統性抖動源
在一個理想中繼器中，信號碼型對輸出定時信號的相位沒有影響。但是，實際的中繼器總會有各種缺陷存在，這就會造成定時信號的相位變化，形成抖動。
- 碼間干擾：目前的光纖製造技術還不能精確地控制光纖的色散特性，而均衡器又不希望做得很複雜，因而少量的碼間干擾是容許的。隨著溫度變化和元器件老化，碼間干擾會增大，使傳輸信號通過非線性元件後引起輸出脈衝峰值位置的隨機偏移，一`形成定時抖動。
- 有限脈寬作用：傳輸信號的脈衝寬度不可能是無限窄的a脈衝序列，因而其頻譜在時鐘附近帶有一段傾斜的連續譜，其傾斜度隨傳輸信息的內容變化而變化。這種時變的斜率將對定時信號進行相位調製，形成抖動。
- 限幅器的門限偏移：限幅器的門限會隨溫度的變化和元器件的老化而偏移。在這種情況下，當不同幅度的信號加到限幅器上時，將與門限的交叉點不再一致，使輸出脈衝位置隨輸人信號的幅度而變化，而輸人信號的幅度與傳輸信息的碼型有關。
- 雷射二極體的碼型效應：在高比特率系統中，由於脈衝重複周期變短，雷射二極體LD的有限通斷時間對傳輸信號的碼型(又稱圖案)的影響增大，而且這種影響隨傳輸信號的碼型不同而異，其結果導致碼型相關抖動。
綜上可知，光纜線路系統中的抖動源及其物理機制十分複雜，很難用精確的數學模型來描述。實際上，儘管各種不同機制的抖動源所引起的抖動譜是不一樣的，但其差異僅表現在高頻細節部分。經過多中繼傳輸後，這些高頻抖動分量均被濾除，只有低頻分量才可能累積起來，進而對系統造成損傷。因此，、為了衡量光中繼器各種抖動源所產生的抖動大小，更直接方法是測量。按照月前的技術水平，典型光中繼器的隨機性抖動均方根值為0.5°~1.5°，系統性抖動均方根值為0.5°~3.5°。總的抖動均方根值大約為1°~4°。
理論模型
在分析傳統電纜數字線路系統抖動積累問題時，Chapman模型是廣泛採用的分析模型。按照這一模型，在多中繼連結的數字線路系統中，所有中繼器都是線性時不變系統。對於由N個相同的中繼器組成的線路系統，則第N箇中繼器的輸出抖動功率譜密度
和輸入抖動功率譜密度
之間滿足下述線性方程：
式中，
是中繼器的抖動傳遞函式，
是中繼器本身產生的抖動功率譜密度，它由隨機性抖動分量
和系統性抖動分量
兩部分組成。近來，Trischitta通過實驗證明，Chapman的線性時不變模型原則上也適用於光纜數字線路系統。下面結合光纜數字線路系統的特點，叔lJ就三種不向類型的抖動積累進行分析。
隨機性抖動的積累
假設隨機性抖動是均值為零的白色吧隨機變數`由於各箇中繼器所產生的這種抖動是彼此無關的，於是經過N個相同的中繼器後所得到的總的積累抖動均方值了
為
這一方程需用數值移分才能求解。但在下述兩種雖然特殊卻經常用的情況下，可以得到封閉解形式。
1、抖動傳遞函式為一階低通濾波器函式形式
當定時濾波器採用單調諧電路亘失諧為零時，其相應抖動傳遞函式
可以表示為：
式中B為抖動傳遞函式的3dB頻寬。將式(3)代人式(2)，經積分後可以得到封閉解如下:
式中
和
分別表示一個中繼器和N箇中繼器的隨機性抖動均方根值。累的隨機性抖動均方根值隨中繼器數目的
遞增。
2、抖動傳遞函式為二階低通濾波器函式形式
在高比特率光纜數字線路系統中，二階低通濾波器是更常用的傳遞函式形式，其數學表達式為：
式中
表示阻尼係數，
是抖動傳遞函式的3dB頻寬角頻率。這類傳遞函式可以用LC調諧電路、二階鎖相環或聲表面波濾波器來實現。當阻尼係數示於0.707時，抖動傳遞函式的幅頻特性出現大於0dB的最大值，稱為抖動峰值。抖動峰值隨
減小而增加。將式(5)代入式(2)，可以得到封閉形式的解答如下：
當中繼器數目很大時，可以將上述公式進一步簡化為：
可見當阻尼係數很小時，隨機性抖動可能隨中繼器數目的指數規律增長，而阻尼係數很大時，則僅隨
增長。為了控制抖動積累，應該取較大的阻尼係數`。這時，無論是一階低通濾波器，還是二階低通濾波器，抖動積累都隨增長。
系統性抖動的積累
系統性抖動泛指各箇中繼器所產生的彼此完全相關的抖動。一般文獻認為，系統性抖動就是碼型相關抖動。實際各箇中繼器定時電路的缺陷不會是完全相同的，信號脈衝形狀也有差異，因而碼型相關抖動可以分解為兩個正交分量：一項為碼型全相關的抖動，稱為系統性抖動，另一項是碼型不相關的抖動，其特性如同隨機噪聲一樣，因而可以歸人隨機性抖動。這樣，由於各箇中繼器所產生的系統性抖動的功率密度譜滬，應按線性疊加，積累的抖動均方值為：
可見，積累的系統性抖動不僅跟抖動傳遞函式的幅頻特性有關，而且還跟相頻特性有關。這一點跟隨機性抖動不同。
1、抖動傳遞函式為一階低通濾波器函式形式。
將式(3)代人式(2)積分可以得到：
利用
函式及其遞推公式和近似展開式，可以將上式進一步簡化為：
該式最大誤差僅1.4%，特別是N值不太大時，比Byrne採用Sitrilgn公式所得到的近似公式精度要高。`當N>=100時，則有
可見，積累的系統性抖動均方根值大致隨杯了關係增長，其速率比隨機性抖動要快得多了。
綜上所述，當抖動傳遞函式沒有峰值時，無論採用一階低通濾波器，還是二階低通濾波器，積累的系統性抖動都隨
關係增長，比隨機性抖動要快得多、但是，當抖動傳遞函式出現峰值時，則系統性抖動也近似按中繼器數目的指數規律遞增，只不過積累速率不如隨機性抖動那么快。
抖動積累的特點
目前，已發表的有關實際光纜線路系統的抖動積累測試數據不多，`所得結果也差異甚大。事實上，:影響抖動積累規律的因素很多，諸如中繼器數目、定時濾波器類型、傳輸信號的線路碼型和抖動傳遞函式形紐貸等等。實際系統的這些參數千差萬別，不可能用一個統一簡單的規律來概括這些影響。但是，就長途光纜數字線路系統而言，下述的幾個特點是值得注意的：
隨機性抖動的影響不容忽視
與傳輸電纜數字線路系統相比，光纜系統不僅增加了一些特有的隨機性抖動源，而且在碼型相關抖動中大約有50%的分量也屬於隨機性抖動，這就使得隨機性抖動在總的抖動量中所占的比重增加。特別是，當抖動傳遞函式有峰值時，隨機性抖動的積累速率甚至會超過系統性抖動，成為主要的部分。
碼型相關抖動不一定按系統牲抖動積累
如前所述，各箇中繼器所產生的碼型相關抖動並非完全相關。實測結果表明，僅有50%是全相關的，仍按系統性抖動積累，而剩餘的50%是完全不相關的，只能按隨機性抖動積累處理。在一個由光纜系統組成的數欄位內，抖動積累效應將有所減弱。
數欄位內總的抖動積累效應有所減弱
這是因為數字復用設備中備有獨立的振盪器產生時鐘，所以前一個數欄位的抖動一般不能進入本數欄位，這樣，抖動主要在一個數欄位內積累。而另一方面，在傳統電纜線路系統中，中繼器間隔只有幾km，而光纜系統可達幾十km，因而對於一個280km的標準數欄位來說，只含有幾個中繼器。顯然，中繼器數目的大大減少意味著抖動積累效應的減弱。這有利於整個系統抖動性能的改善。
總之，在一個設計良好的光纜系統中，抖動積累一般不會簡單地遵循傳統的
規律，而是處於 和
之間。當然，由於實際系統情況千差萬別，得到不同的積累規律不足為怪。圖給出最新發表的美國ATT公司280Mb/s單模光纜系統抖動積累測試結果。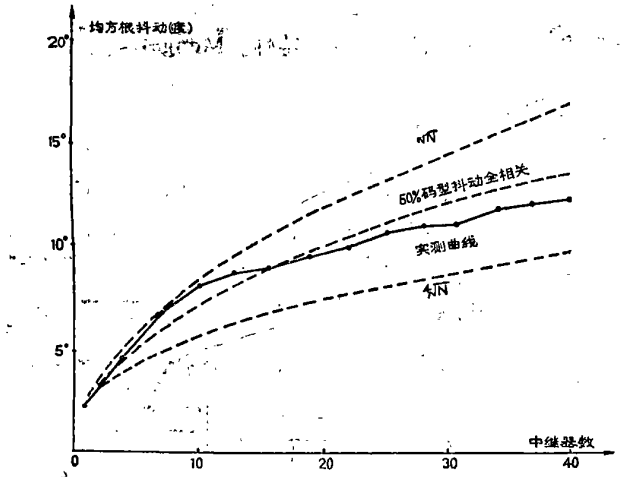
由圖中實測曲線可見，當中繼器數目少於10時，抖動積累按 遞增。而大於10以後，抖動積累逐漸偏離 關係，處於 和 之間。採用修改的chapman模型(如圖中間虛線)後，則計算結果與實測曲線比較吻合。因而，在系統分析時，我們可以採用修改的chapman模型來估算抖動積累特性。
