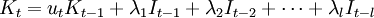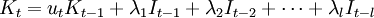投資函式是指在投資領域內，某一變數隨另一變數的變化而變化的數量依存關係。在投資過程中，有許多互相關聯、互相依賴的變數表現為函式關係。如在投資決策中，有預期收益率同投資額兩個變數，投資額隨預期收益率一起變化， 且依賴於預期收益率，則稱該投資額是預期收益率的投資函式。又如一定的淨產值隨一定的勞動力數量、質量的變化而變化（假定其他條件不變），則勞動力數量、質量與淨產值具有函式關係。
基本介紹
- 中文名：投資函式
- 外文名：investment function
- 線性形式： i = e – d r
- 涉及學科：經濟學
詞典解釋,投資理論,函式內容,函式介紹,函式模型,
詞典解釋
投資函式
詞性解釋
investment function
投資理論
當投資的預期利潤率既定時，投資取決於利率： 利率上升，則投資需求量減少； 利率下降，則投資需求量增加。 投資需求是利率的減函式。
函式內容
函式： i= i(r)
d=△i/△r 是指利率上升（下降）一個百分點引起投資減少（增加）的數量。
實際利率：根據實際價值計算的一項金融資產的收益率。
投資函式函式介紹
投資函式是指投資和利率之間的關係：I=b·iI:代表投資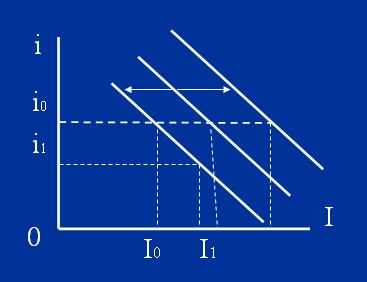
投資曲線的變動
投資曲線的變動i:代表利率
2、投資曲線的變動
函式模型
加速模型
1. 常見4類模型形式
I、Y、K分別表示投資、國民收入、固定資產。
It= f(ΔYt) + μt
It= f(Yt,Kt− 1) + μt
It= f(Yt,Yt− 1,It− 1) + μ
It= f(ΔYt,Yt− 1,It− 1) + μ
分別為後面4類加速模型。
2. 原始加速模型(Naïve Accelerator Model)
1917年Clark提出
K= αY
It= αΔYt+ μ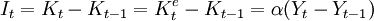
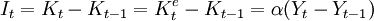
3.靈活的加速模型（Flexible Accelerator Model）
Koyck於1954年
如果考慮到折舊，則有：
It= Kt− Kt− 1 + δKt− 1 = αλYt+ (δ − λ)Kt− 1
It= αλYt+ (δ − λ)Kt− 1 + μ
4.實用的加速模型
利用It− 1 = Kt− 1 + (1 − δ)Kt− 2
It− (1 − δ)It− 1 = αλYt+ (δ − λ)Kt− 1 − (1 − δ)αλYt− 1 − (1 − δ)(δ − λ)Kt− 2
= αλYt− (1 − δ)αλYt− 1 + (δ − λ)It− 1
It= αλYt− (1 − δ)αλYt− 1 + (1 − λ)It− 1 + μ
5.利用最新信息的加速模型
It= αλYt− n− (1 − δ)αλYt− n− 1 + (1 − λ)It− 1
= αλΔYt− n+ δαλYt− n− 1 + (1 − λ)It− 1
It= αλΔYt− n+ δαλYt− n− 1 + (1 − λ)It− 1 + μ
6 對加速模型的評價
假設
(1)沒有資本閒置
資本產出比為常數
不存在自發投資
採用幾何滯後
(2)揭示了投資活動的原動力
(3)從總體上反映了投資活動中的因果關係
(4)具有較大的實際套用價值
利潤決定的投資函式模型
1、假設
加速模型認為投資的原動力是產出的增長。
2、模型
Grunfeld於1961年提出了資本存量的預期值與利潤水平之間的關係：
考慮資本存量的調整過程，投資函式模型為：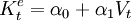
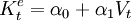
= λα0 + λα1Vt+ (δ − λ)Kt− 1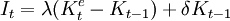
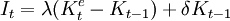
其計量形態為：
It= λα0 + λα1Vt+ (δ − λ)Kt− 1 + μ
先驗地得到折舊率δ，然後估計模型的其它參數。
新古典投資函式模型
1、假設
加速模型假設資本產出比為常數，即認為資本與其它要素之間不具有可替代性。
2、模型
以利潤最大為目標，以新古典生產函式為約束條件，求解如下極值問題：
MzxRt= ptYt− wtLt− wtLt− rtKt
約束：Yt= f(Kt,Lt)
其中R、p、w、r分別為利潤、產品的價格、工資率和資本的租金。
求解該極值問題即得到資本的最優存量，以此決定投資。
該模型的求解過程利用了邊際生產力條件，不適用。
一個中國的投資函式模型
⒈ 模型形式
常用的模型形式
合理的經濟解釋
估計中的問題
⒉ 推導過程 根據經濟行為，有
It= f1(Yt)
Yt= f3(Kt,Lt)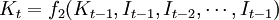
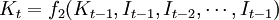
逐一代入，則得到上面所表示的投資函式模型 。
分別採用簡單的線性關係表示上述3個函式，有
It= αtYt
Yt= etKt
