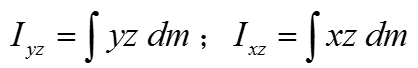慣性積

面積慣性積

面積慣性積　有實際套用價值的只是平面積的慣性積，是截面的一個重要幾何性質。平面積A對平面內互相垂直的x和y軸的慣性積為：

式中x，y為面元dA的位置坐標。面積慣性積常用的單位有厘米和米等。如果一個平面積對x(或y)軸對稱，則I_xy=0（見截面的幾何性質）。

1、截面的慣性積是對相互垂直的一對坐標軸定義的。

2、慣性積的量綱為長度的四次方。

3、慣性積的數值可正可負也可為零。若一對坐標軸中有一軸為截面圖形的對稱軸，則截面對該對坐標軸的慣性積必為零。反之則不成立，即截面的慣性積為零，則該截面相對於某一軸對稱是不成立的。

4、組合截面對某一對坐標軸的慣性積，等於各組分圖形對同一對坐標軸的慣性積的代數和。

質量慣性積是剛體動力學中一個重要的質量幾何性質。剛體中的質量微元 Δm_i與這微元的兩個直角坐標的乘積對剛體的總和。其數值為：

式中x_i、y_i為組成剛體的質量微元Δm_i（或dm）在x、y軸上的坐標；求和號（或積分號）遍及整個剛體。同樣有

慣性積是計算轉動慣量數式的一部分。它也出現於對定軸轉動剛體軸的動反力計算中。慣性張量是二階對稱張量，它可以完整地刻畫剛體繞通過定點 O任一軸的轉動慣量的大小。慣性張量的非對角線分量即為各相應的慣性積。慣性橢球在 O點有三根互相垂直的主軸。如果將直角坐標系Oxyz選在這三根主軸上，則全部慣性積得零。