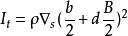慣性半徑（radius of gyration）又稱迴轉半徑，是指物體微分質量假設的集中點到轉動軸間的距離，其值為任一截面對某軸的慣性矩除以該截面面積所得商的平方根值，它的大小也等於轉動慣量除總質量後再開平方。物體在轉動時對慣性的度量稱轉動慣量，它的大小等於物體各微分質量與其到轉動軸的距離平方的乘積之和。
基本介紹
- 中文名：慣性半徑
- 外文名：radius of gyration
- 別稱：迴轉半徑
- 大小：慣性矩除以該截面面積得平方根值
- 概念：微分質量假設集中點到轉動軸距離
- 一級學科：工程技術
基本概念,轉動慣量,估算方法研究,研究介紹,估算公式,
基本概念
若將物體的質量集中到物體的某一點上，則定義均質物體的慣性半徑為：
（1）均質細直桿：
；
（2）均質細圓環：
；
（3）均質圓盤：
。
利用上式，若已知物體的慣性半徑ρz，就可以較方便地計算出物體的轉動慣性為
轉動慣量
剛體對轉軸Z的軸轉動慣量為
其中，
為質量
的第
個質點到轉軸Z的垂直距離。
剛體對轉軸的轉動慣量等於剛體上每個質點的質量與該點到轉軸垂直距離的平方的乘積之和，恆為正值，單位為kg·m2。
剛體的轉動慣量是轉動剛體慣性的量度。若想獲得較大的轉動慣量，應使剛體的質量分布在離轉軸較遠處。例如，起制動作用的飛輪，其質量儘可能地分布在輪緣上；若想獲得較小的轉動慣量，應使質量靠近轉軸，同時應採用較輕的物質。
估算方法研究
研究介紹
近年來，特種排水型高性能船舶的研究趨於活躍，如深 V型船、小水線面雙體船以及穿浪雙體船等，都是研究和使用較多的船型，同時，三體船也引起了人們極大的關注。三體船船型的特殊構造使得高速三體船的興波阻力小，2 個側體又能提供足夠的穩性，且連線橋還具有提高總縱強度的功能，同時也有利於形成寬闊的甲板面，為設備布置提供更大的空間。此外，該船型還具有優良的耐波性，尤其是可避免雙體船的“扭搖”（橫搖與縱搖的耦合搖擺）與“急搖”（短周期的橫搖），並可明顯減小縱搖和升沉。 由於三體船具有這些突出的優點，其特性研究便成為焦點。 三體船的橫搖性能與三體船的穩性關係極大，而橫搖慣性半徑正是橫搖問題的關鍵參數之一。
對於單體船的橫搖慣性半徑的估算值是其船寬的 0.30 ～ 0.40 倍。 對於大部分甲板上沒有貨物或壓載的船舶來說，質量主要集中在船體兩側，對於甲板上有貨物或壓載的船舶而言，貨物的質量分布對慣性半徑的取值有很大的影響，因此船舶在滿載情況下的慣性半徑值要小於空載情況。值得注意的是，如果把船舶簡化成一根長、寬、高與船的長、寬、吃水相同且質量均勻分布的梁，其橫搖慣性半徑的解析值為 0.29 倍的船寬。可見，簡化的單體梁模型的橫搖慣性半徑與實際船的橫搖慣性半徑的取值很接近。也就是說，單體船橫搖慣性半徑可以簡化為質量均勻的單體梁模型橫向慣性半徑乘以小的修正係數。基於這一觀點出發，該研究將三體船簡化為等效的三體梁模型，通過對三體梁簡化模型的研究，給出三體船橫搖慣性半徑的估算公式。
估算公式
估算單體船的橫搖慣性半徑時，是將船體簡化為一根長梁，通過修正長梁的慣性半徑得到估算值。當忽略三體船主側體連線甲板上的重量時，即假定三體船的所有重量是均分在主側體上，則可以將三體船簡化為三根獨立的梁。在簡化後的三體梁模型中，主體梁長 L、寬B、吃水 T，側體梁長 l、寬b、吃水 t，主側體間距為 d（圖1）。
圖1
圖1該三體梁的慣性矩可套用材料力學方法求得。單體慣性矩：
單個側體移軸慣性矩：
總慣性矩：
則三體梁的橫向慣性半徑為：
上式中， ρ 為質量密度；
、
分別為三體梁體積和單個側體梁體積；d 為圖 1所示的主側體間距；Ixxc為主體慣性矩；Ixxs為側體慣性矩；It為側體移軸慣性矩。
