恆星測距法

以公轉軌道半徑為基線，用某種方法測出地球和恆星之間的距離的方法。要計算恆星的距離，首先得知道一個距離單位──光年。光年就是光在一年當中所走過的距離。我們知道光速是30萬千米/秒。那么光在一年當中所走過的距離大約有10萬億千米。天文學家用它作為測量天體距離的單位。

基本介紹

• 中文名：恆星測距法
• 最基本方法：三角視差法
• 隸屬學科：天文學、天體物理學
• 方法種類：10種
• 用途：研究恆星空間位置、求恆星的光度
• 已測定恆星：已經測定了約10000顆恆星

簡介

天文學家利用三角視差法、分光視差法、星團視差法、統計視差法、造父視差法和力學視差法等，測定恆星與我們的距離。恆星距離的測定，對研究恆星的空間位置、求得恆星的光度和運動速度等，均有重要的意義。離太陽距離在16光年以內的有50多顆恆星。其中最近的是半人馬座比鄰星，距太陽約4.2光年，大約是40萬億千米。

目前，用三角視差法己測定了約10000顆恆星的距離，這些恆星視差角都不超過一角秒。更遙遠的恆星視差角非常小，很難確定它們的距離，只有用其他方法來測定了。如分光視差法、星團視差法、統計視差法以及由造父變星的周期光度關係確定視差等。

如果地球不是繞太陽運動的，那么從地球上看同一個恆星就不會有方向上的差異。如果地球是繞太陽運動的，那么從地球上觀測某一顆恆星時，由於地球在其軌道上位置的變化，就必然產生方向上的差異，也就一定會有視差出現，其實，它是相對於更遠的恆星有位移。自從哥白尼提出日心地動學說以後，許多人企圖觀測恆星的視差，以此來證名哥白尼學說是否正確。但是，自哥白尼提出“日心地動”說以後300年間，沒有人測出恆星的周年視差。因此，有人開始懷疑哥白尼學說是否正確。直到1837年—1839年，幾位天文學家終於測出了恆星周年視差，這不僅建立了測量恆星距離的方法，同時也使哥白尼學說建立在更科學的基礎上。

恆星距離

恆星的星等相差很大，這裡面固然有恆星本身發光強弱的原因，但是離開我們距離的遠近也起著顯著的作用。較近恆星離開我們的距離可以用三角方法來測量，在十六世紀哥白尼公布了他的日心說以後，許多天文學家試圖測定恆星的距離，但都由於它們的數值很小以及當時的觀測精度不高而沒有成功。直到十九世紀三十年代後半期，才取得成功。照相術在天文學中的套用使恆星距離的觀測方法變得簡便，而且精度大大提高。自二十世紀二十年代以後，許多天文學家開展這方面的工作，到二十世紀九十年代初，已有8000多顆恆星的距離被用照相方法測定。在二十世紀九十年代中期，依靠“依巴谷”衛星進行的空間天體測量獲得成功，在大約三年的時間裡，以非常高的準確度測定了10萬顆恆星的距離。

恆星的距離，若用千米表示，數字實在太大，為使用方便，通常採用光年作為單位。1光年是光在一年中通過的距離。真空中的光速是每秒30萬千米，乘一年的秒數，得到1光年約等於10萬億公里。離開我們最近的恆星是半人馬星座的南門二星，距離為4.3光年。

恆星距離測量

恆星距離我們非常遙遠，連光都要走好多年。那么，怎樣測量出恆星的距離呢? 測量的方法很多，其中對大量較近的恆星可以採用三角視差法測量，如右圖。地球繞太陽作周年運動，地球和太陽的距離在恆星處的張角稱為“周年視差”，用π表示。地球和太陽的平均距離a是已知的，周年視差π可測定出。這樣，有了a和π恆星和太陽的距離r就很容易求出，即：見最後的圖 （π很小，按直角三角形公式計算）

測量恆星的距離還有其它許多方法，而三角視差法是最基本的方法。

在當今這個電子時代，太陽系的距離測量是不成問題的。人們用雷達測量金星的距離，並且根據約翰內斯·克卜勒發現的“克卜勒第三定律”來分析。這條定律把各行星繞太陽公轉的周期和它們的軌道半徑聯繫了起來，舉例來說，如果A和B各代表一顆行星，比方說金星與地球，那么克卜勒這條定律可寫為

（A的公轉周期）²×（B的軌道半徑）³=（B的公轉周期）²×（A的軌道半徑）³。

行星的公轉周期可以直接由觀測求得（地球365.26天，金星224.70天），所以這條定律為我們提供了一個聯繫兩行星軌道半徑的方程式。

人們能夠把雷達信號從地球發到金星，並且收到由金星反射回來的信號。雷達信號以光速運動，知道了它的傳播時間就可以得到地球與金星的距離，從而求出兩者的軌道半徑差。這樣一來，我們就有了包含地球與金星軌道半徑這兩個未知數的兩個方程式，然後把它們解出來就行了。

下一步是由太陽系過渡到恆星距離的測定。天文學家為此所用的“視差法”早就由伽利略（GalileoGalilei）提出過，但是直到1838年才由弗里德里希·威廉·貝塞爾第一次成功地用來測定天鵝座61號星的距離（這在本書第4章已提到過）。由於地球每年繞太陽公轉一周，我們在一年之中所看到附近恆星在天上的方向老是略有變遷。圖B-1就簡略地表示了這種情況。把地球在1月1日的位置和7月1日的位置這兩點用一條直線連起來，它的長度是已知的，也就是地球軌道半徑的2倍。天文學家只要在這2天觀測某星，就能測出圖B-1中的CAB角和CBA角。這樣，三角形ABC的兩角和一邊已知，用我們在中學裡就已學過的數學可以求出所有未知的角和邊，就是說，也能算出地球和該星在1月1日和7月1日兩個時刻的距離。不過實際上恆星都是極為遙遠，這兩段距離之間的細微差別完全可以忽略不計。

這樣，我們就得出了恆星離太陽系的距離。用了這種方法，人們已經能夠把天體的距離測量伸展到大約300光年的遠處。舉例來說，圖2-2是太陽附近恆星的赫羅圖，其中所有恆星的距離全都是用視差方法測定的。對於更遠的恆星，從地球軌道上相隔半年的兩處望去的方向差值實在太微小，測不出來，這種方法就不靈驗了。

還有一種重要的距離測定法，這裡只大略地講一下。它的依據是，同一個星團中的恆星都在以同樣的速率沿著平行的軌道向同一方向運動。雖然從地球上看去它們在天上的位置變化非常緩慢，很不容易測量出來，但天文學家還是發現了許多星團中群星的平行軌道都有會聚到天上某一點的現象，就像地面平行的火車鐵軌看起來在遠方會聚到一點那樣。這種會聚點告訴我們該群恆星飛向何方。有了這項信息，又用都卜勒效應得到了這些恆星的視向速度，再測出了它們年復一年相對於遙遠背景星的移動角速度，就可以求出它們的距離來。這時的做法也無非就是簡易的解三角形計算。許多星團的距離是這樣測定的。再把這些星的光度求出來，就能夠像第2章中所講的那樣去研究它們在赫羅圖上的分布規律。

我們也不妨反其道而行之。比方說有某個星團離開我們實在太遠，上面所講的各種測定距離的方法都不管用了，那么我們還可以利用兩條規律來解決問題，一條是其中質量較小的恆星位於主序上，另一條是這些星全都滿足主序星所應有的顏色與光度對應關係。這樣一來，只要我能測出這個星團中某一顆主序星的顏色，馬上就能知道它的光度，把光度和這顆星在天上看起來的視亮度加以對比，略作計算，我就能求出這顆星的，也就是這個星團的距離。

實際上人類已經能夠測量的距離遠遠超出了上述範圍，這樣的成就簡直是一種奇蹟。由於人們長期不了解的原因，脈動著的造父變星表現出一種奇異的規律性：脈動周期和光度存在單一的對應關係。造父變星的脈動周期只要耐心觀測就很好測定，馬上就能得出它在一個脈動周期中的平均光度；把這一數值和我們觀測到天上此星的平均亮度加以對比，隨即就可算出它的距離。造父變星的本身光度非常強，它們不僅可見於銀河系的邊遠角落，而且明暗交替的變化還使它們顯眼於河外星系的眾星之間。人類利用了造父變星已經突破銀河系，超出了仙女座大星系，把測量距離的探索擴向更遠得多的空間。

恆星距離列表

太陽 - 距離地球8光分（1天文單位或0.000 016光年）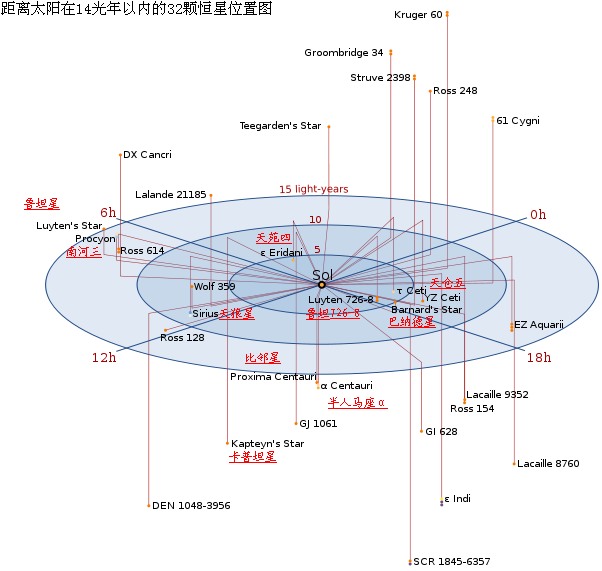

近距離恆星

距離太陽在15光年以內的38顆恆星，由近至遠排列：

1、南門二恆星系

比鄰星 （半人馬座 V645) - 距離4.2421光年 視星等11.09

半人馬座α A/B - 距離4.3650光年 視星等0.01/1.34

2、巴納德星 （蛇夫座）- 距離5.9630光年 視星等9.53

3、Wolf 359 （沃夫359 獅子座） - 距離7.7825光年 視星等13.44

4、拉蘭德21185 （大熊座） - 距離 8.2905光年 視星等7.47

5、天狼星（大犬座α) A/B - 距離8.5828光年 視星等−1.43/11.34

6、魯坦 726-8 A（鯨魚座 BL)/B(鯨魚座UV星)- 距離8.7280光年 視星等12.54/12.99

7、Ross 154 (V1216 Sagittarii)- 距離9.6813光年 視星等10.43

8、Ross 248 (HH Andromedae)- 距離10.322光年 視星等12.29

9、波江座 ε（天苑四，εEri)- 距離10.522光年 視星等3.73

10、Lacaille 9352- 距離10.74231光年 視星等7.37

11、Ross 128 （羅斯128，室女座） - 距離 10.919光年 視星等11.13

12、EZ Aquarii（寶瓶座EZ恆星系，魯坦 789-6) A/B/C- 距離11.266171光年 視星等13.33/13.27/14.03

13、南河三（小犬座 α） A/B- 距離11.402光年 視星等0.38/10.70)

14、天鵝座 61 (61 Cygni) A/B- 距離11.403光年 視星等5.21/6.03

15、Struve 2398 A/Struve 2398 B - 距離11.525光年 視星等8.9/9.69)

16、Groombridge 34 A /Groombridge 34 B- 距離11.624光年 視星等8.08/11.06

17、印第安座ε A/Ba/Bb- 距離11.624光年 視星等4.69/>23/>23

18、DX Cancri （巨蟹座DX）- 距離11.826光年 視星等14.78

19、τ Ceti (天倉五，鯨魚座τ星，Tau Ceti） - 距離 11.887光年 視星等3.49

20、GJ 1061 - 距離11.991光年 視星等13.09

21、YZ Ceti （鯨魚座YZ星 12.132光年 視星等12.02

22、魯坦星 （小犬座）- 距離12.366光年 視星等9.86

23、Teegarden's star- 距離12.514光年 視星等15.14

24、SCR 1845-6357 A/B （孔雀座） - 距離 12.571光年 視星等17.39/?

25、卡普坦星（繪架座，2003年發現） - 距離 12.777光年 視星等8.84

26、Lacaille 8760 - 距離12.870光年 視星等6.67

27、Kruger 60 A/B - 距離13.149光年 視星等9.79/11.41

28、DEN 1048-3956- 距離13.167光年 視星等17.39

29、Ross 614 A/B- 距離13.349光年 視星等11.15/14.23

30、Gl 628- 距離13.820光年 視星等10.07

31、Van Maanen's Star- 距離14.066光年 視星等12.38

32、Gl 1- 距離14.231光年 視星等8.55

33、Wolf 424 A/B- 距離14.312光年 視星等13.18/13.17

34、TZ Arietis- 距離14.509光年 視星等12.27

35、Gl 687- 距離14.793光年 視星等9.17

36、LHS 292 - 距離14.805光年 視星等15.60

37、Gl 674 - 距離14.809光年 視星等9.38

38、GJ 1245 A/B/C- 距離14.812光年 視星等13.46/14.01/16.75

*注 A/B 指雙星系統， A/B/C 指三星系統。

注釋：這些距離是近星研究團體（Research Cnsrtium n Nearby Stars，Recns）發表的視差測量數據。這些數據的來源分別是：耶魯視差表[Y]、Hipparcs星表[H]、Sderhjelm 1999[S]、Tinney 1996 [T]。

天體測量方法

光譜在天文研究中的套用

人類一直想了解天體的物理、化學性狀。這種願望只有在光譜分析套用於天文後才成為可能並由此而導致了天體物理學的誕生和發展。通過光譜分析可以：

⑴確定天體的化學組成；

⑵確定恆星的溫度；

⑶確定恆星的壓力；

⑷測定恆星的磁場；

⑸確定天體的視向速度和自轉等等。

天體距離的測定

人們總希望知道天體離我們有多遠，天體距離的測量也一直是天文學家們的任務。不同遠近的天體可以采不同的測量方法。隨著科學技術的發展，測定天體距離的手段也越來越先進。由於天空的廣袤無垠，所使用測量距離單位也特別。天文距離單位通常有天文單位（AU）、光年（ly）和秒差距（pc）三種。

月球與地球的距離

月球是距離我們最近的天體，天文學家們想了很多的辦法測量它的遠近，但都沒有得到滿意的結果。科學的測量直到18世紀（1715年至1753年）才由法國天文學家拉卡伊（N.L.Lacaille）和他的學生拉朗德（Larand）用三角視差法得以實現。他們的結果是月球與地球之間的平均距離大約為地球半徑的60倍，這與現代測定的數值（384401千米）很接近。

雷達技術誕生後，人們又用雷達測定月球距離。雷射技術問世後，人們利用雷射的方向性好，光束集中，單色性強等特點來測量月球的距離。測量精度可以達到厘米量級。

太陽和行星的距離

地球繞太陽公轉的軌道是橢圓，地球到太陽的距離是隨時間不斷變化的。通常所說的日地距離，是指地球軌道的半長軸，即為日地平均距離。天文學中把這個距離叫做一個“天文單位”（1AU）。1976年國際天文學聯合會把一個天文單位的數值定為1.49597870×10¹¹米，近似1.496億千米。

太陽是一個熾熱的氣體球，測定太陽的距離不能像測定月球距離那樣直接用三角視差法。早期測定太陽的距離是藉助於離地球較近的火星或小行星。先用三角視差法測定火星或小行星的距離，再根據克卜勒第三定律求太陽距離。1673年法國天文學家卡西尼（Dominique Cassini）首次利用火星大沖的機會測出了太陽的距離。

許多行星的距離也是由克卜勒第三定律求得的，若以1AU為日地距離，“恆星年”為單位作為地球公轉周期，便有：T²=a³。若一個行星的公轉周期被測出，就可以算出行星到太陽的距離。如水星的公轉周期為0.241恆星年，則水星到太陽的距離為0.387天文單位（AU）。

恆星的距離

由於恆星距離我們非常遙遠，它們的距離測定非常困難。對不同遠近的恆星，要用不同的方法測定。目前，已有很多種測定恆星距離的方法：三角視差法，分光視差法，分光視差法，造父周光關係測距法，譜線紅移測距法

恆星測量方法

三角視差法

河內天體的距離又稱為視差，恆星對日地平均距離（a）的張角叫做恆星的三角視差（p），則較近的恆星的距離D可表示為：sinπ=a/D

若π很小，π以角秒表示，且單位取秒差距（pc），則有：D=1/π

用周年視差法測定恆星距離，有一定的局限性，因為恆星離我們愈遠，π就愈小，實際觀測中很難測定。三角視差是一切天體距離測量的基礎，至今用這種方法測量了約10，000多顆恆星。

天文學上的距離單位除天文單位（AU）、秒差距（pc）外，還有光年（ly），即光在真空中一年所走過的距離，相當94605億千米。三種距離單位的關係是：

1秒差距（pc）=206265天文單位（AU）=3.26光年=3.09×10¹³千米

1光年（1y）=0.307秒差距（pc）=63240天文單位（Au）=0.95×10¹³千米。

分光視差法

對於距離更遙遠的恆星，比如距離超過110pc的恆星，由於周年視差非常小，無法用三角視差法測出。於是，又發展了另外一種比較方便的方法--分光視差法。該方法的核心是根據恆星的譜線強度去確定恆星的光度，知道了光度（絕對星等M），由觀測得到的視星等（m）就可以得到距離。

m - M= -5 + 5logD.

造父周光關係測距法

大質量的恆星，當演化到晚期時，會呈現出不穩定的脈動現象，形成脈動變星。在這些脈動變星中，有一類脈動周期非常規則，中文名叫造父。造父是中國古代的星官名稱。仙王座δ星中有一顆名為造父一，它是一顆亮度會發生變化的“變星”。變星的光變原因很多。造父一屬於脈動變星一類。當它的星體膨脹時就顯得亮些，體積縮小時就顯得暗些。造父一的這種亮度變化很有規律，它的變化周期是5天8小時46分38秒鐘，稱為“光變周期”。在恆星世界裡，凡跟造父一有相同變化的變星，統稱“造父變星”。

1912 年美國一位女天文學家勒維特（Leavitt 1868--1921）研究小麥哲倫星系內的造父變星的星等與光變周期時發現：光變周期越長的恆星，其亮度就越大。這就是對後來測定恆星距離很有用的“周光關係”。目前在銀河系內共發現了700多顆造父變星。許多河外星系的距離都是靠這個量天尺測量的。

譜線紅移測距法

20 世紀初，光譜研究發現幾乎所有星系的都有紅移現象。所謂紅移是指觀測到的譜線的波長（l）比相應的實驗室測知的譜線的波長（l0）要長，而在光譜中紅光的波長較長，因而把譜線向波長較長的方向的移動叫做光譜的紅移，z=(l-l0)/ l0。1929年哈勃用2.5米大型望遠鏡觀測到更多的河外星系，又發現星系距我們越遠，其譜線紅移量越大。

譜線紅移的流行解釋是大爆炸宇宙學說。哈勃指出天體紅移與距離有關：Z = H*d /c，這就是著名的哈勃定律，式中Z為紅移量；c為光速；d為距離；H為哈勃常數，其值為50～80千米/（秒·兆秒差距）。根據這個定律，只要測出河外星系譜線的紅移量Z，便可算出星系的距離D。用譜線紅移法可以測定遠達百億光年計的距離。

威爾遜-巴普法

1957年，O.C.威爾遜和巴普兩人發現，晚型（G、K和M型）恆星光譜（見恆星光譜分類）中電離鈣的反轉發射線寬度的對數與恆星的絕對星等之間存在著線性關係。對這條譜線進行光譜分析，便可得到晚型恆星的距離。

星際視差法

在恆星的光譜中出現有星際物質所產生的吸收線。這些星際吸收線的強度與恆星的距離有關：星越遠，星和觀測者之間存在的星際物質越多，星際吸收線就越強。利用這個關係可測定恆星的距離。常用的星際吸收線是最強的電離鈣的K線和中性鈉的D雙線。不過這個方法只適用於O型和早B型星，因為其他恆星本身也會產生K線和D線，這種譜線同星際物質所產生的同樣譜線混合在一起無法區分。由於星際物質分布不均勻，一般說來，用此法測得的距離，精度是不高的。

力學視差法

目視雙星的相對軌道運動遵循克卜勒第三定律，即伴星繞主星運轉的軌道橢圓的半長徑的立方與繞轉周期的平方成正比。設主星和伴星的質量分別為m1和m2，以太陽質量為單位表示，繞轉周期P以恆星年（見年）為單位表示，軌道的半長徑的線長度A以天文單位表示，這種雙星在觀測者處所張的角度 α以角秒表示，則其周年視差π為：，

式中α和P可從觀測得到。因此，如果知道雙星的質量，便可按上述公式求得該雙星的周年視差。如果不知道雙星的質量，則用疊代法解上式，仍可求得較可靠的周年視差。周年視差的倒數就是該雙星以秒差距為單位的距離。

星群視差法

移動星團的成員星都具有相同的空間速度。由於透視作用，它們的自行會聚於天球上的一點或者從某點向外發散，這個點稱為“輻射點”。知道了移動星團的輻射點位置，並從觀測得到n個成員星的自行μk 和視向速度V 噰（k=1,2，…，n），則該星團的平均周年視差為：

式中θk為第k個成員星和輻射點的角距，堸 為 n個成員星的空間速度的平均值。這樣求得的周年視差的精度很高。但目前此法只適用於畢星團。其他移動星團因距離太遠，不能由觀測得到可靠的自行值。

統計視差法

根據對大量恆星的統計分析資料，知道恆星的視差與自行之間有相當密切的關係：自行越大，視差也越大。因此對具有某種共同特徵並包含有相當數量恆星的星群，可以根據它們的自行的平均值估計它們的平均周年視差。這樣得到的結果是比較可靠的。

自轉視差法

銀河系的較差自轉（即在離銀河系核心的距離不同處，有不同的自轉速率）對恆星的視向速度有影響。這種影響的大小與星群離太陽的距離遠近有關，因此可從視向速度的觀測中求出星群的平均距離。這個方法只能套用於離太陽不太遠，距離大約在1,200秒差距以內的恆星。

測定天體的距離是天體測量最重要的研究課題之一，儘管方法很多，但要得到可靠的結果是不容易的。因此，對於某一天體，應儘可能採用幾種方法分別測定它的距離，然後相互校核，才能得到可靠的結果。

雷射測距

測程方程

Pr=(Pt*Kt*Kr*Ar*p*r*m)exp(-2zR)/πR²

Pt：雷射測距機的發射功率W Kt：發射光學系統的投射率 Ar：接收孔徑面積 p：目標漫反射係數 z：大氣或其他介質的單程投射率 Kr：接收光學系統的投射率Pr：雷射測距機的接收峰值功率 R：目標距離

r=β²/θ²（β=θ）註：β接收視場角 θ：發射光束髮散角

m=4*σ*cosφ/πθ²R² （σ*cosφ=（πθ²R²)/4）註：σ：目標面積 φ：目標面積法線於發射光束之間的夾角。