顧名思義,快速冪就是快速算底數的n次冪。其時間複雜度為 O(log2N), 與樸素的O(N)相比效率有了極大的提高。
基本介紹
- 中文名:快速冪
- 外文名:Fast Power
- 時間複雜度:log(n)
- 性質:快速算底數的n次冪
原理,實現,代碼比較,
原理
以下以求a的b次方來介紹
把b轉換成二進制數。
該二進制數第i位的權為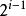
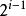
例如
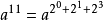
11的二進制是1011
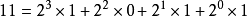
因此,我們將a11轉化為算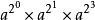
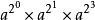
實現
快速冪可以用位運算來實現
b and 1{也就是取b的二進制最低位(即第0位) 判斷b是否為奇數,是則為1} b shr 1{就是去掉b的二進制最低位(即第0位)} C++實現為
b & 1//取b二進制的最低位,判斷和1是否相同,相同返回1,否則返回0,可用於判斷奇偶
b>>1//把b的二進制右移一位,即去掉其二進制位的最低位
以下為pascal的實現:
var a,b,n:int64;function f(a,b,n:int64):int64;var t,y:int64;begin t:=1; y:=a; while b<>0 do begin if(b and 1)=1 then t:=t*y mod n; y:=y*y mod n;{這裡用了一個技巧,y*y即求出了a^(2^(i-1))不知道這是什麼的看原理 a^(2^(i-1))*a^(2^(i-1))=a^(2^i) 而且一般情況下a*b mod c =(a mod c)*(b mod c) mod c} b:=b shr 1;{去掉已經處理過的一位} end; exit(t);end;begin read(a,b,n);{n是模} writeln(f(a,b,n));end.以下為C的實現,為了方便與pascal的對照,變數全部與上面相同.可以對照查看。
遞歸版:
ll pow(ll a,ll i){ if (i==0) return 1; int temp=pow(a,i>>1); temp=temp*temp%MOD; if (i&1) temp=(ll)temp*a%MOD; return temp%MOD;}非遞歸版:
ll f(ll a,ll b,ll n){ int t,y; t=1; y=a; while (b!=0){ if (b&1==1) t=t*y%n; y=y*y%n; b=b>>1; } return t;}代碼比較
常規求冪
int pow1(int a,int b){ int r=1; while(b--) r*=a; return r;} 快速求冪(一般)
int pow2(int a,int b){ int r=1,base=a; while(b!=0){ if(b%2) r*=base; base*=base; b/=2; } return r;}快速求冪 (遞歸)
int f(int m,int n){ //m^n if(n==1) return m; int temp=f(m,n/2); return (n%2==0 ? 1 : m)*temp*temp;}快速求冪(位運算)
int pow3(int x,int n){ if(n==0) return 1; else { while((n&1)==0){ n>>=1; x*=x; } } int result=x; n>>=1; while(n!=0){ x*=x; if(n&1) result*=x; n>>=1; } return result;}完整快速冪代碼
#include<bits/stdc++.h>using namespace std;long long qiuckpower(long long x,long long y){ long long ans=1,cnt=x; while(y) { if(y&1) { ans*=cnt; } cnt*=cnt; y>>=1; } return ans;}int main(){ long long x,y,ans; cin>>x>>y; ans=qiuckpower(x,y); cout<<ans; return 0;}
