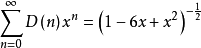德蘭諾依數描述了從(0,0)到(m,n)的格路問題中,只允許按照(0,1)、(1,0)或者(1,1)的方式移動,一共有多少不同的方案數。
基本介紹
- 中文名:德蘭諾依數
- 外文名:Delannoy number
定義,示例,德蘭諾依數組,計算,
定義
在組合數學中,德蘭諾依數描述了從(0,0)到(m,n)的格路問題中,只允許按照(0,1)、(1,0)或者(1,1)的方式來走,一共有多少不同的方案數。德蘭諾依數是以法國軍官、業餘數學家亨利·德蘭諾依的名字命名的。
示例
當m=3,n=3時,德蘭諾依數D(3,3)=63,下面展示了所有63種不同方案。

德蘭諾依數組
德蘭諾依數組以矩陣形式展示了不同m,n組合下的德蘭諾依數。
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
| 2 | 1 | 5 | 13 | 25 | 41 | 61 | 85 | 113 | 145 |
| 3 | 1 | 7 | 25 | 63 | 129 | 231 | 377 | 575 | 833 |
| 4 | 1 | 9 | 41 | 129 | 321 | 681 | 1289 | 2241 | 3649 |
| 5 | 1 | 11 | 61 | 231 | 681 | 1683 | 3653 | 7183 | 13073 |
| 6 | 1 | 13 | 85 | 377 | 1289 | 3653 | 8989 | 19825 | 40081 |
| 7 | 1 | 15 | 113 | 575 | 2241 | 7183 | 19825 | 48639 | 108545 |
| 8 | 1 | 17 | 145 | 833 | 3649 | 13073 | 40081 | 108545 | 265729 |
| 9 | 1 | 19 | 181 | 1159 | 5641 | 22363 | 75517 | 224143 | 598417 |
從上述矩陣中可以發現如下有趣的性質:
- 關於主對角線對稱。
- 第1行(列)均為1。
- 第2行(列)均為奇數。
- 第3行(列)均為中心正方形數(OEIS A001844)。
- 第4行(列)均為中心正八面體數(OEISA001845)。
- 以左上角為頂點,構成了帕斯卡三角。
中心德蘭諾依數
中心德蘭諾依數是指m=n時的德蘭諾依數,即D(n,n).該數列的前幾項為
1, 3, 13, 63, 321, 1683, 8989, 48639, 265729,.....(OEIS A001850)
計算
假設對角線方向(1,1)一共走了k步,那么x方向(1,0)必為(m-k)步,y方向(0,1)必為(n-k)步,且三個方向上的順序可以任意調整。
故
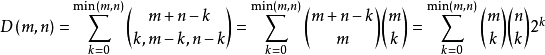
D(m,n)的遞推關係可以寫為
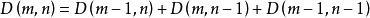
當m=0或n=0時,D(m,n)=1。
由遞推關係可寫出其生成函式為:
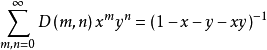
對於中心德蘭諾依數,

中心德蘭諾依數的遞推關係為

由遞推關係求出其生成函式為