復判定係數及R2=1-SSE/SST(其中SSE為殘差平方和，SST為總平方和)是用來說明因變數的變動中可以用自變數來解釋的比例。它可以反映模型的好壞，但由於隨著自變數的增加，SSE只會減少，不會變大，而對給定的一組變數觀察值來說SST卻總是恆定不變，故變數引進模型只會導致R2增大而不會縮小，這極易使人產生錯覺，似乎自變數越多越好。其結果是過多引進一些效率不高的自變數。而統計量1-((n-1)/(n-p-1).(SSE/SST))稱為調整的復判定係數，當自變數增加，SSE減小時，其自由度n-p-1就變小，這樣調整的復判定係數就不會象R2那樣自變數越多越大，從而可能避免引進過多的不必要的自變數，使自變數的選擇更合理。
基本介紹
- 中文名：復判定係數
- 外文名：Coefficient of multipl edetermination
- 所屬學科：數學
- 所屬問題：數理統計
- 簡稱：判定係數
- 別稱：多重判定係數
- 相關概念：多元線性回歸，離差平方和等
- 相關介紹：調整後的復判定係數
基本介紹,調整後的判定係數,判定係數與調整後的判定係數的關係,
基本介紹
復判定係數是指在多元線性回歸分析中，回歸離差平方和占總離差平方和的比重，一般也稱為多重判定係數(multiple coefficient of determination)，或簡稱為判定係數。
與一元線性回歸的情形一樣，多元線性回歸的復判定係數的計算公式是：
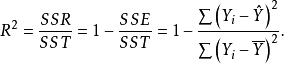
R2表示因變數Y的全部變差中可由
的差異解釋的部分所占的比例。
回歸方程的精度與簡潔性的標準往往不可能同時得到最大化的滿足。在回歸方程精度的測量指標中，最常用的指標是復判定係數。復判定係數的一個重要性質是，它是出現在模型中的自變數個數的非減函式，即隨著自變數個數的增大，R2幾乎必然增大，至少是不減小。為了看清楚這一點，我們先看R2的計算公式：
公式中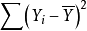
與模型中X變數的個數沒有關係，但
與自變數的個數有關，直觀上，隨著X變數個數的增加，其很可能減小(至少不會增大)，隨之R2會相應增大。這一變化也可通過圖1所示的圖形表現出來。
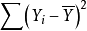
圖1判定係數變化圖調整後的判定係數
建立回歸模型時，不能一味地通過增多自變數的個數來實現回歸精度的提高。因為判定係數逐步提高的過程，回歸方程也就逐漸背離了其簡潔的原則。因而在對回歸方程進行評價時需要進行綜合的考慮和評價。即在考慮模型精度的同時也要考慮模型的簡潔性。進行模型的評價或模型的比較時，必須要考慮到模型中出現的自變數的個數，計算調整後的判定係數
。
調整是指對判定係數R2計算公式中平方和所涉及的自由度的調整，在一個涉及p+1個參數的模型中，SSE有n-p-1個自由度，而SST有n-1個自由度。
判定係數與調整後的判定係數的關係
從式子中可以看到：
1)p>1時，
，這意味著增加X變數的個數，調整後的比未調整的
增加的慢些。
2)雖然R2必定是非負的，但可以是負的。
調整後的判定係數與自變數個數之間的關係如圖2所示。
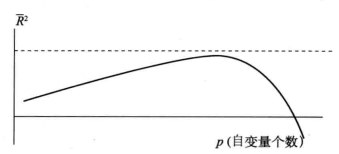圖2 調整後判定係數變化圖根據判定係數，不管是通過調整後的還是未經調整的判定係數來比較兩個模型，一定要注意樣本大小n和因變數都必須相同，而自變數可以採取不同的形式與內容。例如：
因為按定義，R2度量的是因變數的變異可以由自變數解釋的部分，所
中R2度量的是X1和X2解釋
的變異部分；而
中的
度量的是X1和X2解釋Y的變異部分，兩者不是同一回事，兩個判定係數所度量的不是同一問題。
進行多元線性回歸模型的比較與評價最常用的測量指標是調整後的判定係數，此外，還有其他的準則，包括赤池的信息準則(Akaike Information Criterion，AIC)和施瓦茨準則(Schwarz Criterion，SC)等。
