基本介紹
簡介
形狀識別的一般流程
一、形狀提取
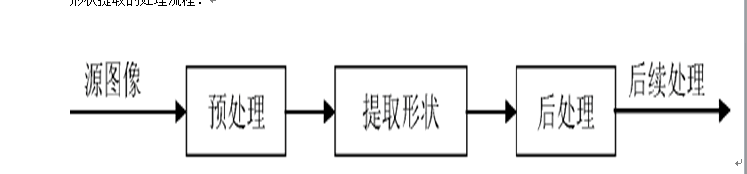
 圖1
圖1
二、形狀特徵提取
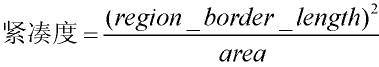
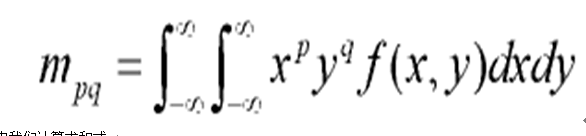
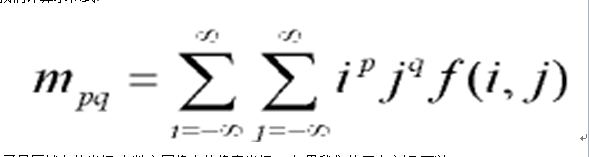
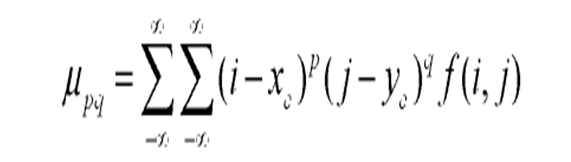



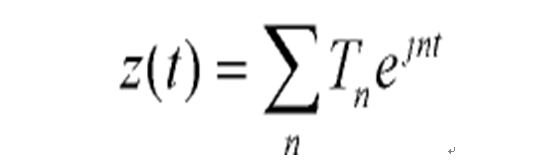
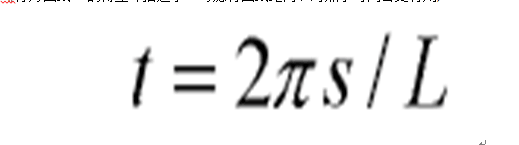
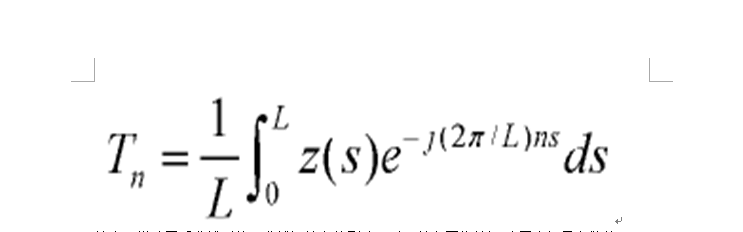

三、分類識別
二、形狀特徵提取
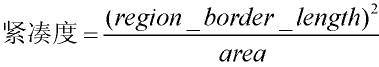
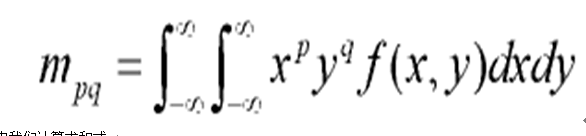
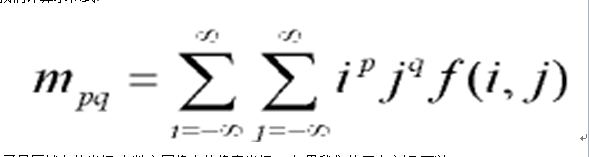
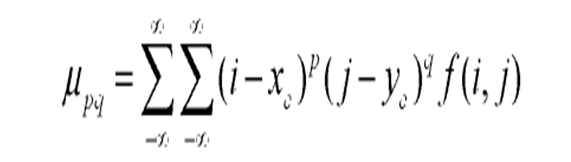



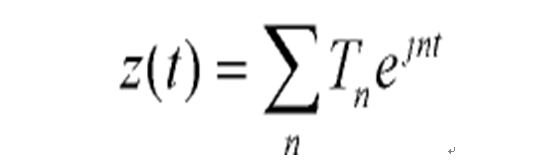
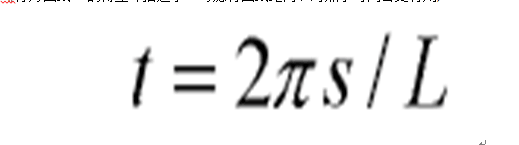
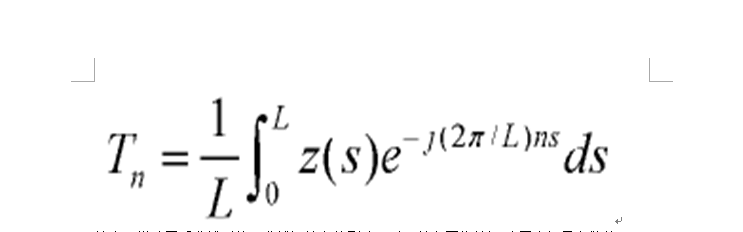



 圖1
圖1
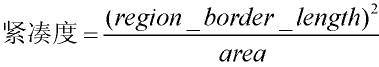
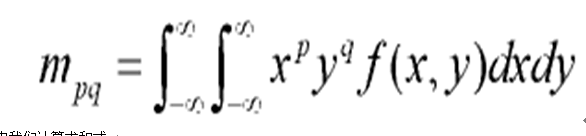
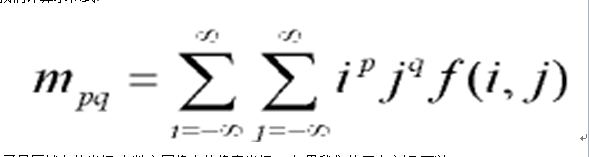
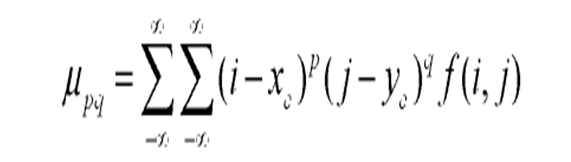



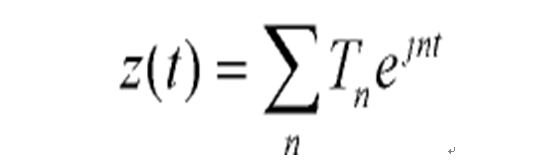
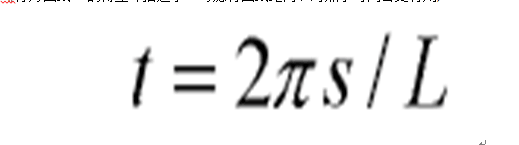
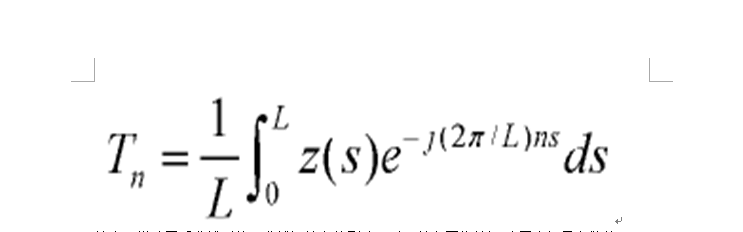

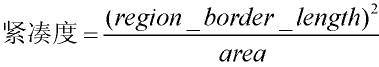
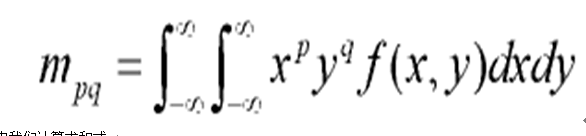
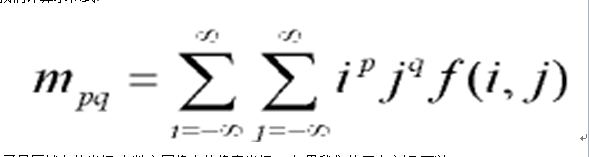
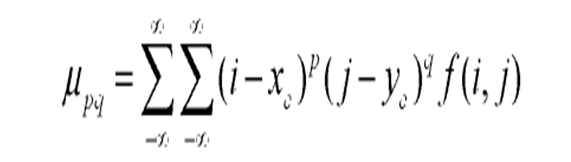



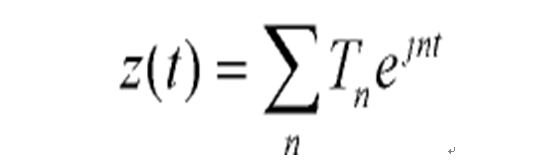
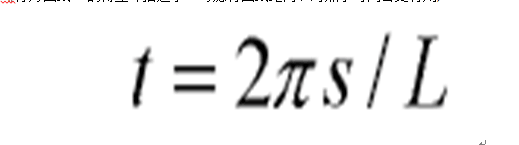
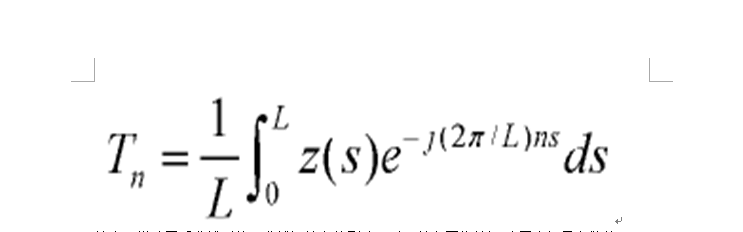

物體的形狀識別是模式識別的重要方向,廣泛套用於圖像分析、機器視覺和目標識別等領域。目前,對形狀識別的主要方法有傅立葉描述子、主分量分析等。簡介 物體的形狀識別是模式識別的重要方向,在計算機中物體的形狀有多種表示方式,基於不同...
在當今所處的這個信息爆炸的時代,計算機圖形識別已經成為計算機視覺技術的一個重要研究分支,同時也是圖像檢索的重要基礎。圖像的局部特徵是用於識別的關鍵,在提供更多圖像細節信息、提供對象語義支持基礎以及遮擋條件下對象識別等方面展現出特...
《顏色和形狀的識別》是一款IOS平台的套用。套用介紹 孩子是祖國的未來.在當今這個變化萬千的多元化社會,孩子的教育比以往任何一個時代都要艱巨,如何啟發孩子的智力,能力,知識,怎樣讓孩子更加活潑健康地成才,如何利用當今掌上智慧型設備(智慧型...
手形識別系統(手形儀)是採集手指的三維立體形狀進行身份識別,由於手形特徵穩定性高,不易隨外在環境或生理變化而改變,使用方便,在過去的幾十年中獲得了廣泛的套用。...
人的圖像識別能力是很強的。圖像距離的改變或圖像在感覺器官上作用位置的改變,都會造成圖像在視網膜上的大小和形狀的改變。即使在這種情況下,人們仍然可以認出他們過去知覺過的圖像。甚至圖像識別可以不受感覺通道的限制。例如,人可以用...
在已知圖像物體邊界的條件下抽取物體形態特徵的方法。 形狀分析在圖像特徵抽取和識別中有廣泛的套用。中文名 形狀分析 傅立葉 反映邊界的不規則性, 基元表示 兩相鄰碼的方向差45° 矩和主軸計算 給定邊界內的圖像數據陣列值 ...
這種模型認為,識別某個圖像,必須在過去的經驗中有這個圖像的記憶模式,又叫模板。當前的刺激如果能與大腦中的模板相匹配,這個圖像也就被識別了。例如有一個字母A,如果在腦中有個A模板,字母A的大小、方位、形狀都與這個A模板完全一致...
特徵識別 特徵識別(feature recognition)是2018年全國科學技術名詞審定委員會公布的計算機科學技術名詞。定義 從產品的幾何模型中自動識別出具有一定工程語義的幾何形狀。出處 《計算機科學技術名詞 》第三版。
對物體形狀的識別開始於對原始特徵的分析與檢測。這些原始特徵包括點、線條、角度、朝向和運動等。視覺系統對這些特徵的檢測是自動的,無需意識的努力。特性 形狀的特徵分析 許多心理學家相信,對形的識別開始於對原始特徵的分析與檢測。
幾何模式識別是指利用一些幾何特性對表征事物或現象的各種形式的信息進行處理和分析。例如圖像模式識別中常用周長、面積、圓形度、離心率等這些形狀變數進行模式識別。簡介 幾何模式識別是指利用一些幾何特性對表征事物或現象的各種形式的信息...
環形碼是類似於圓環狀的槍靶形狀,又稱牛眼碼。由於可編碼的信息容量小,印製困難,現在套用較少。但是由於圓環形不受方向的限制,所以仍受到人們的重視。符號識別過程 (1)在被識別的物體表面上按一定的規格或形式列印上編碼符號。常見...
這種模型認為,識別某個圖像,必須在過去的經驗中有這個圖像的記憶模式,又叫模板。當前的刺激如果能與大腦中的模板相匹配,這個圖像也就被識別了。例如有一個字母A,如果在腦中有個A模板,字母A的大小、方位、形狀都與這個A模板完全...
邊緣識別又稱邊緣檢測,是模仿人類視覺的一個過程。在檢測物體邊緣時, 先對其輪廓點進行粗略檢測, 然後通過連結規則把原來檢測到的輪廓點連線起來, 同時也檢測和連線遺漏的邊界點及去除虛假的邊界。邊緣檢測的目的是去發現圖像中關於形狀和...
標誌形狀(shape of sign)是傳遞特定交通信息的幾何形狀。選用的基本原則是易辨認性。容易識別辨認的形狀順序是三角形、菱形、正方形、矩形、五角形、圓形、六角形等。常用的為以下幾種:(扮三角形。視認性最好,可作警告標誌。(2)圓形...
手勢分析是完成手勢識別系統的關鍵技術之一。通過手勢分析,可獲得手勢的形狀特徵或運動軌跡。手勢的形狀和運動軌跡是動態手勢識別中的重要特徵,與手勢所表達意義有直接的關係。手勢分析的主要方法有以下幾類: 邊緣輪廓提取法、質心手指等多...
王忠禮使用高階不變矩陣提取人耳圖像的特徵進行識別。加利福尼亞大學的Bir Bhanu和Hui Chen使用range感測器獲取的range人耳圖像帶有三維幾何形狀信息,使用local surface patches(LSP)來描述人耳,提出了基於3D圖像的人耳識別方法。當人耳...
地物的形狀是識別它們的重要而明顯的標誌。不少地物往往可以直接根據它特殊的形狀加以判定,如河曲、沖洪積扇、果園、火山錐、雷達站等。影像大小,指地物尺寸、面積、體積在圖像上的記錄,是地物識別的重要標誌,它直觀地反映地物目標...
孩子們通過認識日常生活中的事物,如它們的形狀、顏色、圖案,以及學習動物的名字和聲音,進而增強孩子們聯想、邏輯、空間和視覺思維能力。 孩子們在遊戲中可以給小動物們穿衣服,給動物們它們喜歡吃的食物,給蝴蝶找回丟失的翅膀等等。拔...
人的圖像識別能力是很強的。圖像距離的改變或圖像在感覺器官上作用位置的改變,都會造成圖像在視網膜上的大小和形狀的改變。即使在這種情況下,人們仍然可以認出他們過去知覺過的圖像。甚至圖像識別可以不受感覺通道的限制。例如,人可以用...
脈衝形狀鑑別法 在用某些閃爍體進行粒子測量時可用此方法。其原理是:帶電粒子在閃爍體中激發螢光,螢光的衰減時間與致激發的帶電粒子種類有關(見閃爍計數器)。例如,脫氧有機閃爍體中質子激發的螢光衰減時間比電子激發的長得多。這...
例如,如果要補間一張正在改變表情的臉部圖畫時,可以使用形狀提示來標記每隻眼睛。這樣在形狀發生變化時,臉部就不會亂成一團,每隻眼睛還都可以辨認,並在轉換過程中分別變化。使用形狀提示 形狀提示包含字母(從 a 到 z),用於識別...
物理識別是指對目標物的物理、化學和生物學的量化認識。如視覺包括明暗、色彩、大小、形狀、遠近、受力、活力、運動狀態等。聽覺包括聲音的大小、頻率、方位、波形等;觸覺包括溫度、硬度、濕度、狀態等;嗅覺和味覺包括物質的組成及化學成...
對象識別過程 對象識別系統使用訓練圖像,訓練出識別模型 ,並利用這個模型識別新圖像中的對象 ,這個過程一般包括預處理 、特徵提取、模型訓練和對象識別四個階段。特徵提取 特徵提取提取圖像的亮度模式,紋理細節、形狀和輪廓等信息,包括...
我根據這些字母的組成及形狀編成順口溜,製成ppt課件,展示給學生,並運用形狀和順口溜的方式讓學生記憶深刻,這樣做就能達到區分形近拼音字母的讀音。設計思路 怎樣幫助學生有效的區分像“bd ”、“pq ”這樣相似的拼音字母的讀音呢?我...
①幾何方法,利用圖像中某一目標的幾何特徵得到亞像素精度的測量數據, 一般是利用圖像中一些規則形狀的目標, 如圓、三角形、正方形等形狀, 但這種算法精度較低, 對不規則形狀的圖像效果不好。②矩估計方法, 由於矩是基於積分的運算, ...
人們在視覺判斷時,除感受色調、色相的差別外,通過形狀和位置的辨認也可以獲得大量的信息。遙感圖像也是如此,一般僅僅依賴光譜信息不易獲得很高的識別精度,只有充分利用了空間結構等圖像信息,才能更好地區分地物。隨著地球資源衛星技術的...
紋理特徵,主要是指比紋線更短、更細的一些紋線,但其在手掌上分布是毫無規律的。掌紋的特徵還包括幾何特徵:如手掌的寬度、長度和幾何形狀,以及手掌不同區域的分布。掌紋中所包含的信息遠比一枚指紋包含的信息豐富,利用掌紋的紋線...
輪廓檢測指在包含目標和背景的數字圖像中,忽略背景和目標內部的紋理以及噪聲干擾的影響,採用一定的技術和方法來實現目標輪廓提取的過程。它是目標檢測、形狀分析、目標識別和目標跟蹤等技術的重要基礎。研究現狀 目前輪廓檢測方法有兩類,一...
