基本介紹
簡介,彌散斑參數的定義,彌散斑測試系統的工作原理,圖像處理算法,背景閾值估計,區域填充,橢圓擬合,
簡介
點光源（即星點）經過光學系統後在像面前後不同截面上所成的衍射像的光強分布即為彌散斑。理想的星點成像時像平面前後的光強呈對稱分布，並隨著視場不同而變化；而實際光學系統成像時，像差等缺陷很容易破壞這種對稱性。彌散斑能量的分布情況能夠非常靈敏地反映光學的像差和缺陷，因此定量測量彌散斑參數是控制光學系統成像質量的重要手段。
目前，定量化測量彌散斑參數的需求主要集中於星敏感器光學系統的研製中。星敏感器是一種高精度的姿態測量設備，因其角秒量級的姿態測量精度而廣泛地套用於衛星等各類太空飛行器中。星敏感器可拍攝視場範圍內的星空圖像，通過星點識別提取和星點中心判定完成星圖匹配，實現太空飛行器空間姿態的測定。
星敏感器主要由光學系統和圖像感測器組成。為了獲得大視場範圍的星空圖像，星敏感器的光學系統一般為廣角鏡頭，焦距較小，焦面處的星點像為亞像素級，不易識別。為了提高星點識別的幾率和星點中心判定的精度，星敏感器光學系統常離焦使用或在光學系統中加進球差，使得星空中的星點成彌散像，故彌散斑成像特性是星敏感器光學系統的關鍵指標，其測量也成為研究重點。
彌散斑的定量化參數測量是採用CCD顯微測量系統進行的。該方法利用光學手段將彌散斑放大，不僅提高了系統採樣率，而且有利於後續的圖像處理和分析。合理的圖像處理算法是保證CCD顯微測量彌散斑參數的關鍵。
彌散斑參數的定義
由標量衍射理論可知，理想光學系統在像平面所成的星點像的能量分布為：
式中：
為軸上點的強度，
為一階貝塞爾函式，
為波數，a為光學系統孔徑光闌的半徑，θ為衍射角。
在光學系統光軸方向離焦後，星點像形成彌散斑。彌散斑參數包括彌散斑直徑和彌散斑圓度。彌散斑直徑是指全視場範圍內、合適的離焦量下，對彌散斑能量分布做閉合的能量等高線，與能量占總能量一定比例的能量等高線所形成的閉合區域面積相等的圓直徑，即等效圓直徑。在某些特殊的套用場合，如星敏感器測量太空飛行器姿態時，需要通過軸上離焦使得彌散斑擴散到探測器的多個像元，但要避免軸外彌散斑擴散太大而使彌散斑能量密度太小，此時探測器無法進行探測。因此在全視場範圍內、合適的離焦量下，彌散斑的直徑D要滿 足：包 含A%能 量 的 閉 合 區 域
，包含B%能量的閉合區域
，且B>A，
。彌散斑直徑反映了彌散斑的能量集中度。
彌散斑圓度是指在全視場範圍內、合適的離焦量下，能量占總能量一定比例的能量等高線所形成的閉合區域。過彌散斑質心，在等高線上取正交兩個方向的弦長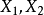
，若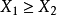
，則彌散斑圓度φ為：
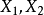
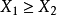
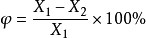
一般要求φ≤20%。彌散斑圓度反映了能量在與光軸垂直的平面內正交方向的分布情況，體現了彌散斑受彗差、像散等的影響程度。
彌散斑測試系統的工作原理
採用CCD顯微測量系統的彌散斑參數測量系統如圖所示。
彌散斑參數的CCD顯微測量系統離軸拋物面平行光管和其焦平面處的帶星點孔的光源模擬無窮遠的點目標，經被測光學系統成像於其焦平面附近，CCD顯微測量系統在被測光學系統的光軸方向離焦採集星點像，即得到彌散斑。高精度轉台提供不同的視場角，以得到不同視場下的彌散斑。其中，星點孔直徑、顯微物鏡的數值孔徑和放大倍率、CCD像元尺寸的選定均要滿足被測光學系統彌 散 斑測試空 間 採樣的要求。CCD的動態範圍、靈敏度、光譜回響要滿足被測光學系統彌散斑能量量化的要求。彌散斑直徑D的計算公式為：
式中：
為彌散圓直徑的測量值，K為顯微物鏡的放大倍率，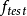
為被測光學系統的焦距，
為離軸拋物面平行光管的焦距，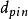
為離軸拋物面平行光管焦面處的星點孔的直徑。
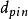
圖像處理算法
通過CCD顯微測量系統採集彌散斑，對被測光學系統一定離焦量後的彌散斑圖像進行圖像處理。
背景閾值估計
背景閾值B主要反映在一定的曝光時間和增益下CCD的回響特性和噪聲水平。背景閾值的選取關係到彌散斑和背景的分離及彌散斑總能量的計算。
採用基於灰度直方圖的閾值算法來統計背景區域的噪聲特性，實現了自適應的背景閾值選取。背景閾值B為：
式中：T為背景灰度中出現機率最大的灰度，即最可幾灰度；Z是與CCD曝光時間、增益相關的參數；sgn為背景灰度的標準偏差。
自適應選定背景閾值實現了彌散斑區域的選取，減小了CCD回響特性和噪聲水平對測試結果的影響。不含彌散斑區域及背景區域的灰度直方圖如圖所示。
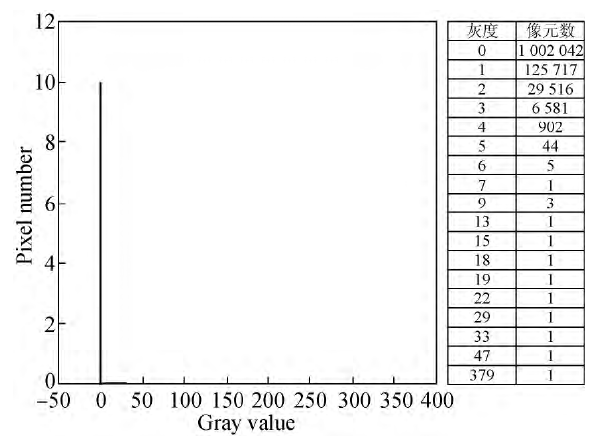背景區域的灰度直方圖分析灰度直方圖可知，該區域的灰度主要分布在0～6，最可幾灰度T為0，灰度的標準偏差sgn為0.62，Z取10，背景閾值B取整後為6。
區域填充
在提取彌散斑形成的連通區域時，由於CCD噪聲和CCD量化誤差的影響，連通區域的邊緣附近會出現孤立的散點，使邊緣不平滑。採用區域填充可消除孤立散點的影響。區域填充也稱為條件膨脹，區域和區域的邊界可以互求，給定區域的邊界點集A及其補集AC，通過結構元Q對其進行膨脹、求補和求交來填充區域。
區域填充的效果如圖所示。圖中，灰色區域為區域填充後形成的閉合區域，白色散點為去背景後的邊緣噪點。
區域填充橢圓擬合
鑒於星點像的能量分布含一階貝塞爾函式，而一階貝塞爾函式是定義圓域的函式。即考慮離焦和像差的影響，又不失一般性，可對連通區域的邊緣進行橢圓擬合。橢圓的一般表達式為：
式中：x,y為邊界點的橫、縱坐標，a,b,c,d,e為係數，f為常數項。由橢圓的一般表達式不能直接地得到表征橢圓幾何特徵的參數，因此要通過求解橢圓的幾何參數，才能得到表征橢圓幾何特徵的參數：橢圓的中心點坐標、長軸、短軸、旋轉角。
橢圓的擬合結果如圖所示。圖中星點構成的閉合曲線為包含總能量80%的能量等高線，實心點構成的橢圓為橢圓擬合後的結果，中心區域的星點為彌散斑質心，中心區域的實心點為總能量80%的能量等高線擬合後的橢圓形心。從圖中可以看出，該橢圓的形心與彌散斑的質心偏離不大，這說明該彌散斑主要受像散影響。
橢圓擬合橢圓的中心點坐標與彌散斑質心的偏離、旋轉角主要反映了彗差的影響。橢圓的短軸與長軸的相對偏差體現了像散的影響。擬合連通區域的邊緣橢圓得到橢圓的幾何參數，可更詳盡地評價彌散斑像差，為光學系統成像質量的控制和分析提供指導。
