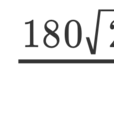張氏圓周率算法

圓周率（Pi）是圓的周長與直徑的比值，一般用希臘字母π表示，是一個在數學及物理學中普遍存在的數學常數。π也等於圓形之面積與半徑平方之比。是精確計算圓周長、圓面積、球體積等幾何形狀的關鍵值。

圓周率用字母 （讀作pài）表示，是一個常數（約等於3.141592654），是代表圓周長和直徑的比值。它是一個無理數，即無限不循環小數。

基本介紹

• 中文名：張氏圓周率計算方法
• 外文名：ZHANGπ
• 別稱：張π
• 表達式：見圖
• 提出者：張皓涵
• 提出時間：2015年
• 套用學科：數學
• 適用領域範圍：三角學
• 適用領域範圍：幾何學

定律定義

π=180*（根號下2-2cosinex）/x當x→0+的極限

張氏圓周率計算方法的Latex表示和MathMl表示方法

MathML的表示方法

推導過程

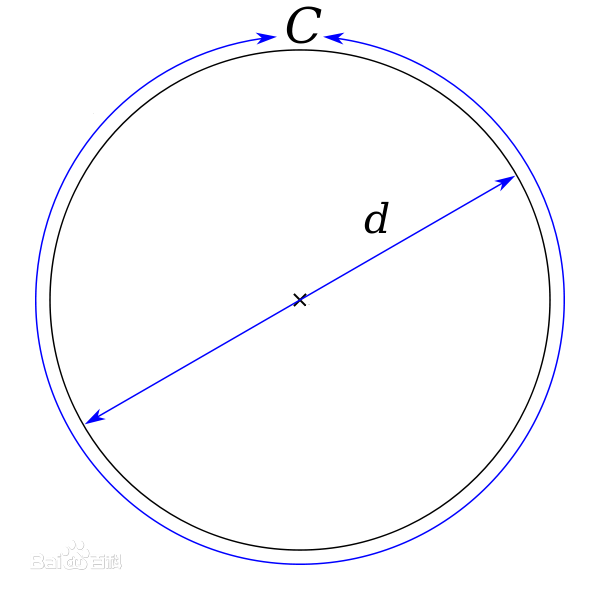
在圓內接正n邊形（n∈N+3），當n→∞時，C多邊形與C圓近似相等，用多邊形的周長除以圓的直徑的得數即為π。

張氏圓周率算法的LaTeX表示方法

實驗驗證

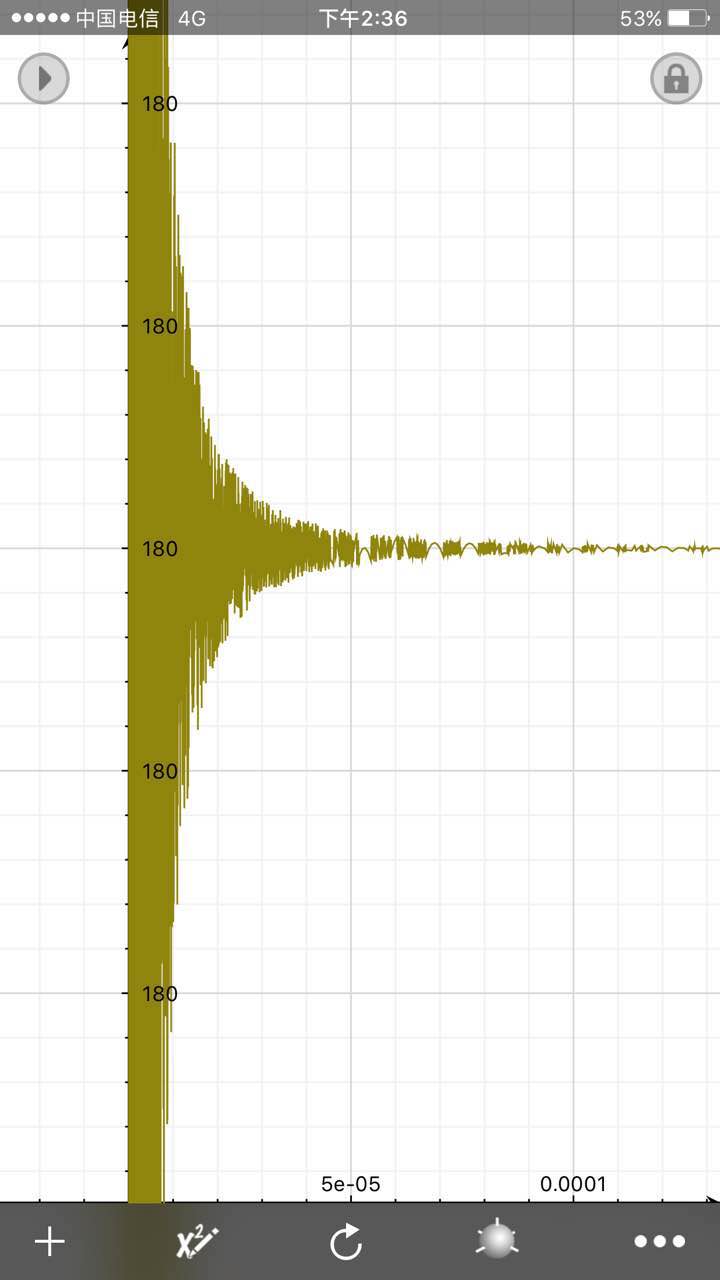
通過描繪該函式的函式圖像所得，當x→0時，該函式的角度值為180，弧度值即為π。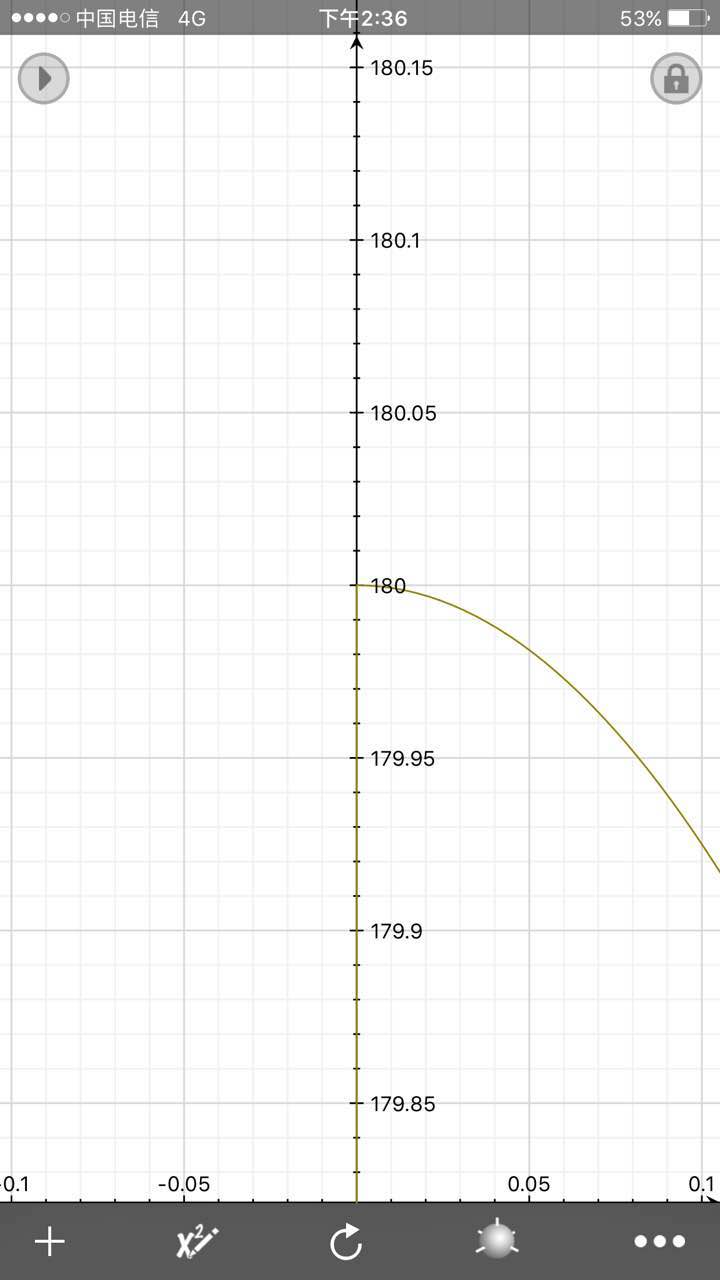

適用範圍

幾何學圓周率的精確套用

三角函式的套用

培養數學的興趣愛好

定律影響&定律誤區

在函式圖像縮小到一定值時，會出現如圖所示的情形，有一段不可描述的函式圖像，圖像的單調性複雜程度異常。