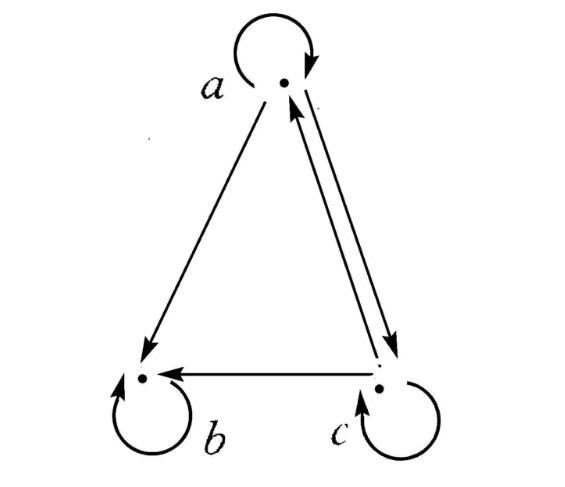
弱序關係(weak-ordering relation)亦稱弱優選關係，是一種重要的二元關係，指集合A中的自反的、傳遞的、連通的二元關係R。弱序關係R對任何a，b∈A，有aRb或bRa，A稱為弱序集，全序是一種弱序，弱序若還是反對稱的，則就是全序。弱序集雖然是強連通的，但一般不能排成一行。
基本介紹
- 中文名：弱序關係
- 外文名：weak-ordering relation
- 所屬學科：數學（集合論）
- 別名：弱優選關係
- 所屬問題：樸素集合論（有序集和序結構）
基本概念,弱序的上界,弱序的等值集,
基本概念
所謂的二元關係(Binary Relation)是指，將兩個事物聯繫在一起的某種特徵，例如：
a是b的兄弟
c位於d的左方
e比f大
g偏好(優)於h
i等於j
我們可以在上述字母之間放置某種符號來表示它們之間所存在的二元關係,例如
可以表示“a是b的兄弟”。在定義該關係時，必須先定義該關係是在什麼樣的域(Domain)上被定義。
下面將給出一些非常有用的定義。
自反性(Reflexivity) 令R表示定義在集合S上的一個關係，若對所有的x∈S，有xRx，則稱關係R為自反的。若定義關係域中的所有元素都可將此關係返回其自身，則該關係是自反的。例如，相等關係(=)就是自反的。
傳遞性(Transitivity) 若xRy和yRz蘊涵xRz，則稱二元關係R為傳遞的。例如，相等關係就是傳遞的，在由實數R構成的集合中,大於關係(>)也是傳遞的。
弱序(Quasi-orderings) 一個具有自反性和傳遞性的二元關係稱為一個弱序。可以選用任意一個方便的標記符號來表示一個弱序關係。表示弱序的常用符號是
。在由實數R構成的集合中。大於或等於關係(≥)就是一個典型的弱序關係。如下面的箭頭圖表示集合A={a，b，c}上的關係R是弱序，既非全序又非偏序，因為有aRc，cRa，但a≠c。
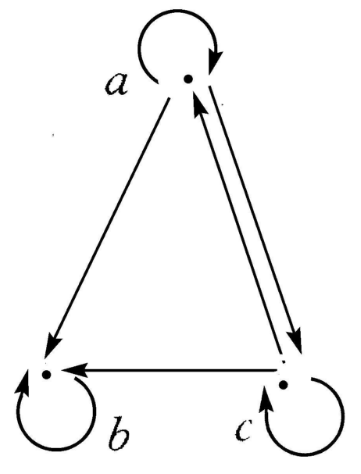
圖1
關係的完備性 只是定義在集合S上的一個關係，若對每一x，y∈S，xRy或yRx關係成立，或者有兩種關係同時成立，則稱關係只是完備的。若關係R按一個方向；或另一相反方向，或同時兩個方向定義了集合S中元素構成的所有序偶之間的相互關係，則定義在集合S上的關係只是完備的。若關係R對由集合S中元素構成的所有序偶都有定義，則關係只是完備的。
弱序的上界
弱序的上界(UpperBound) 令集合S已被弱序關係定義；令X⊂S，若存在y∈S
滿足任一x∈X，yx，則稱y是x的一個上界。令Y={y|yx，所有x∈X}，若存在y’∈Y滿足所有y∈Y，yy'，則稱y'為X的最小上界。
請讀者注意，無論何時，只要X⊂R有一個上界，則X總有一個最小上界，這是有弱序(≥)定義的實數R所具有的一個性質。
弱序的等值集
相似地，可以定義在弱序關係下y的下等值集。
在弱序關係下，所有次於y的點構成的集合稱為y的下等值集：G(y)={x|x∈S，yx}。
