基本介紹
- 中文名：康托展開
- 外文名：Cantor expansion
- 提出者：康托
- 套用學科：計算機科學
- 適用領域範圍：解決一些序列問題的算法
原理介紹,康托展開運算,康托展開和逆康托展開,康托展開舉例,代碼實現,逆康托展開舉例,代碼實現,用途,
原理介紹
康托展開運算
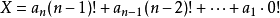
其中,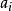
為整數,並且
。
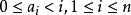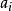
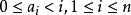
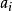
z康托展開的逆運算
既然康托展開是一個雙射，那么一定可以通過康托展開值求出原排列，即可以求出n的全排列中第x大排列。
如n=5,x=96時：
首先用96-1得到95，說明x之前有95個排列.(將此數本身減去1)用95去除4! 得到3餘23，說明有3個數比第1位小，所以第一位是4.用23去除3! 得到3餘5，說明有3個數比第2位小，所以是4，但是4已出現過，因此是5.用5去除2!得到2餘1，類似地，這一位是3.用1去除1!得到1餘0，這一位是2.最後一位只能是1.所以這個數是45321。
按以上方法可以得出通用的算法。
康托展開和逆康托展開
康托展開舉例
再舉個例子說明。
在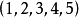
5個數的排列組合中，計算 34152的康托展開值。
在
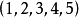
首位是3，則小於3的數有兩個，為1和2，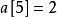
，則首位小於3的所有排列組合為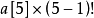
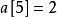
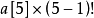
第二位是4，由於第一位小於4，1、2、3中一定會有1個充當第一位，所以排在4之下的只剩2個，所以其實計算的是在第二位之後小於4的個數。因此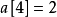
。
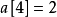
第三位是1，則在其之後小於1的數有0個，所以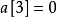
。
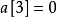
第四位是5，則在其之後小於5的數有1個，為2，所以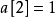
。
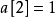
最後一位就不用計算啦，因為在它之後已經沒有數了，所以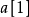
固定為0
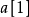
根據公式：
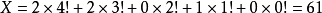
所以比34152小的組合有61個，即34152是排第62。
代碼實現
#include<iostream>using namespace std;const int factorial[]={1,1,2,6,24,120,720,5040,40320,362880,3628800};//階乘0-10int cantor(int a[],int n){//cantor展開,n表示是n位的全排列，a[]表示全排列的數（用數組表示） int ans=0,sum=0; for(int i=1;i<n;i++){ for(int j=i+1;j<=n;j++) if(a[j]<a[i]) sum++; ans+=sum*factorial[n-i];//累積 sum=0;//計數器歸零 } return ans+1;}int main(){ int sb[12],gs; cin>>gs; for(int i=1;i<=gs;i++) cin>>sb[i]; cout<<cantor(sb,gs);//輸出該集合在全排列所在位置 return 0;}逆康托展開舉例
一開始已經提過了，康托展開是一個全排列到一個自然數的雙射，因此是可逆的。即對於上述例子，在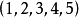給出61可以算出起排列組合為34152。由上述的計算過程可以容易的逆推回來，具體過程如下：
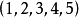
用 61 / 4! = 2餘13，說明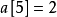
,說明比首位小的數有2個，所以首位為3。
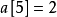
用 13 / 3! = 2餘1，說明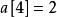
，說明在第二位之後小於第二位的數有2個，所以第二位為4。
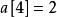
用 1 / 2! = 0餘1，說明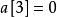
，說明在第三位之後沒有小於第三位的數，所以第三位為1。
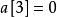
用 1 / 1! = 1餘0，說明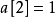
，說明在第四位之後小於第四位的數有1個，所以第四位為5。
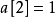
最後一位自然就是剩下的數2。
通過以上分析，所求排列組合為 34152。
代碼實現
static const int FAC[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; // 階乘//康托展開逆運算void decantor(int x, int n){ vector<int> v; // 存放當前可選數 vector<int> a; // 所求排列組合 for(int i=1;i<=n;i++) v.push_back(i); for(int i=n;i>=1;i--) { int r = x % FAC[i-1]; int t = x / FAC[i-1]; x = r; sort(v.begin(),v.end());// 從小到大排序 a.push_back(v[t]); // 剩餘數里第t+1個數為當前位 v.erase(v.begin()+t); // 移除選做當前位的數 }}#include<iostream>#include<cmath>//pow的頭檔案 using namespace std;const int factorial[]={1,1,2,6,24,120,720,5040,40320,362880,3628800};//階乘0-9int gs,rank;//gs表示gs位的全排列，rank排列位置 bool used[11];//判斷是否用過 int decantor(int x,int gs){//逆cantor展開，x就是rank int ans=0;//存放答案 int sum=0;//暫時的計數 int quotient,remainder;//quotient商，remainder餘數 for(int i=gs-1;i>=1;i--){ quotient=x/factorial[i]; remainder=x%factorial[i]; for(int j=1;j<=gs;j++){ if(!used[j]) sum++; if(sum==quotient+1){//找到該位 ans+=j*pow(10,i);//pow冪運算 sum=0;//清零 x=remainder; used[j]=true;//標記為用過 break; } } } for(int i=1;i<=gs;i++){ if(!used[i]){ ans+=i; break; } }//最後一位 return ans;//答案 }//逆推過程 int main(){//（signed main也可以） for(int i=1;i<=10;i++) used[11]=false;//初始化為未用過 cin>>gs; cin>>rank; rank--;//原rank前的個數 cout<<decantor(rank,gs);//輸出該排列 return 0;//建議加上 }用途
顯然，n位（0~n-1）全排列後，其康托展開唯一且最大約為n!，因此可以由更小的空間來儲存這些排列。由公式可將X逆推出唯一的一個排列。
