平穩可逆域

凡使ARMA(p， q)模型φ(B)y_t=θ(B)a_t中，φ(B) = 0,θ (B)=0的根均在單位圓外，φ(B)與θ(B)無公共因子，其相應的自回歸與滑動平均的係數向量φ' = (φ₁,φ₂，...， φ_p)與θ = (θ₁，θ₂，... ，θq)所構成的集合，稱為ARMA (p，q)模型的平穩域和可逆域。當ARMA(p，q)模型的階數p和q不超過2時，模型的平穩域和可逆域都可具體的解析表示出來。但當p、q大於2吋，計算模型的平穩域和可逆域就比較複雜。

基本介紹

• 中文名：平穩可逆域
• 所屬學科：數學
• 所屬問題：統計學（時間序列）

基本介紹

設ARMA (p， q)模型的方程為

其中，，若的根均在單位圓外，且φ (B)，θ (B)無公共因子，則稱此模型為平穩可逆的自回歸滑動平均模型。

ARMA (p，g) 的平穩可逆域：

凡使ARMA (p，q)模型中，的根均在單位圓外，φ (B)與θ(B)無公共因子，其相應的自回歸與滑動平均的係數向量與所構成的集合，稱為ARMA (p，q)模型的平穩域和可逆域。

例題解析

例1求ARMA (1，1)模型的平穩可逆域。

如果ARMA(p，g)模型的自回歸參數屬於平穩域，同時滑動平均參數屬於可逆域，我們就稱ARMA (p，g)模型的參數屬於平穩可逆域內。因此ARMA(1， 1)模型參數的平穩可逆域為

如圖1所示。

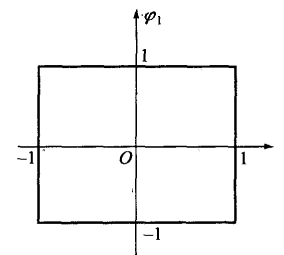
圖1

例2 試求模型AR(1)和ARMA(1，q)的平穩城。

解： 由知φ(B)=1←φ₁B相應的特徵方程為，其根為z=φ_i，|z|<1， 郎|φ₁|<1，所以AR(1)和ARMA(1，q)模型的平穩域為。