平均絕對離差

平均絕對離差(mean absolute deviation)簡稱“平均離差”，當總體的單位數為N時，有變數X₁，X₂，X₃，……，X_N一1，X_N，各項變數與總體平均數之差叫離差，平均絕對離差定義為各數據與平均值的離差的絕對值的平均數。

基本介紹

• 中文名：平均絕對偏差
• 外文名：mean absolute deviation
• 別稱：平均偏差，平均離差等
• 相關概念：組中值等

定義

平均絕對離差(mean absolute deviation)是用樣本數據相對於其平均值的絕對距離來度量數據的離散程度。平均絕對離差也稱為平均離差(mean deviation)。平均絕對離差定義為各數據與平均值的離差的絕對值的平均數。

設樣本的n個觀測值為 ，平均絕對離差為：

對於分組數據，平均絕對離差為：

其中 分別為第 組數據的頻數及組中值， 為數據分組的組數。

例1設有數據：1920，1700，1250，1150，1090，1041，1020，980，950，900，870，計算可得中位數仍為1041，IQR=1250—950=300。Q₁、Q₃、IQR的結果如圖2—15所示。從數據的散布情況看，該組數據集中於中位數的周圍。

解：對於例1所示的數據，由式(1)計算，可得：。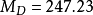

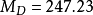
與此相近的還有一種叫“平均差”的尺度，其定義為各變數與樣本的中位數差的絕對值的平均數。

例2某縣黃牛的胸圍記錄是138.7，147.7，149.4，150.4，151.7cm，這時它們的中位數 ，平均差可用下式求出：

平均差、方差和標準差運用了全部觀測值，與極差和IQR相比，在方法上做了一定的改進。但相對而言，平均絕對離差用得較少，在套用中用的較多的是方差和標準差，以便於估計總體的方差和標準差。

平均離差的性質

平均離差作為散布特徵，其含義直觀且便於理解，但是因含絕對值而不便於計算。此外，平均離差用於統計推斷時，其統計性質也遠不如標準差優良，因此在統計推斷中，平均離差比標準差用得較少，這裡指出如下兩條性質：

(1)對於任意常數c，有

其中是中位數。

(2)平均離差可以按如下公式計算：