帶花樹開花算法是在一般圖中構建最大匹配的圖形。該算法由Jack Edmonds於 1961 年提出並於 1965 年發表。給定一個通用圖 G = ( V , E ),該算法找到該圖的一個最大匹配。匹配是通過沿圖中的增廣路徑疊代改進初始空匹配來構建的。不像二部匹配,關鍵的新思想是將圖中的奇數循環(開花)收縮到單個頂點,在收縮的圖中繼續疊代搜尋。
基本介紹
- 中文名:帶花樹開花算法
- 外文名:Edmonds' blossom algorithm
- 適用領域:自然科學
定義,性質,算法理解,搜尋增廣路徑,開花和收縮,
定義
帶花樹開花算法是在一般圖中構建最大匹配的圖形。給定一個通用圖 G = ( V , E ),該算法找到該圖的一個最大匹配。匹配是通過沿圖中的增廣路徑疊代改進初始空匹配來構建的。不像二部匹配,關鍵的新思想是將圖中的奇數循環(開花)收縮到單個頂點,在收縮的圖中繼續疊代搜尋。
性質
算法的最差時間複雜度為O(|E| |V|^2),其中|E|是圖的邊數,|V|是它的頂點數,在算法進行更改後時間複雜度可以降至O(|E||V|^1/2)
開花算法很重要的一個主要原因是它首次證明了可以使用多項式計算時間找到最大大小的匹配。另一個原因是它導致了匹配多面體的線性規劃多面體描述,產生了最小權重匹配的算法,是多面組合學的一個突破。
算法理解
整體算法流程如下

整體算法流程圖
搜尋增廣路徑
若P是圖G中一條連通兩個未匹配頂點的路徑,並且屬於M的邊和不屬於M的邊(即已匹配和待匹配的邊)在P上交替出現,則稱P為相對於M的一條增廣路徑。如果圖是一個二分圖,則利用此方法即可找到相應的最大匹配。但是在普通圖中,由於圖可能會有奇環,因此可能會造成矛盾情況,此時就需要把進行下一步操作
開花和收縮
奇環中有 2k+1 個點,所以最多有 k 組匹配,也就是說有一個點沒有匹配,即這個點在環內兩邊的連邊都不是匹配邊,也只有這個點可以向環外連邊。
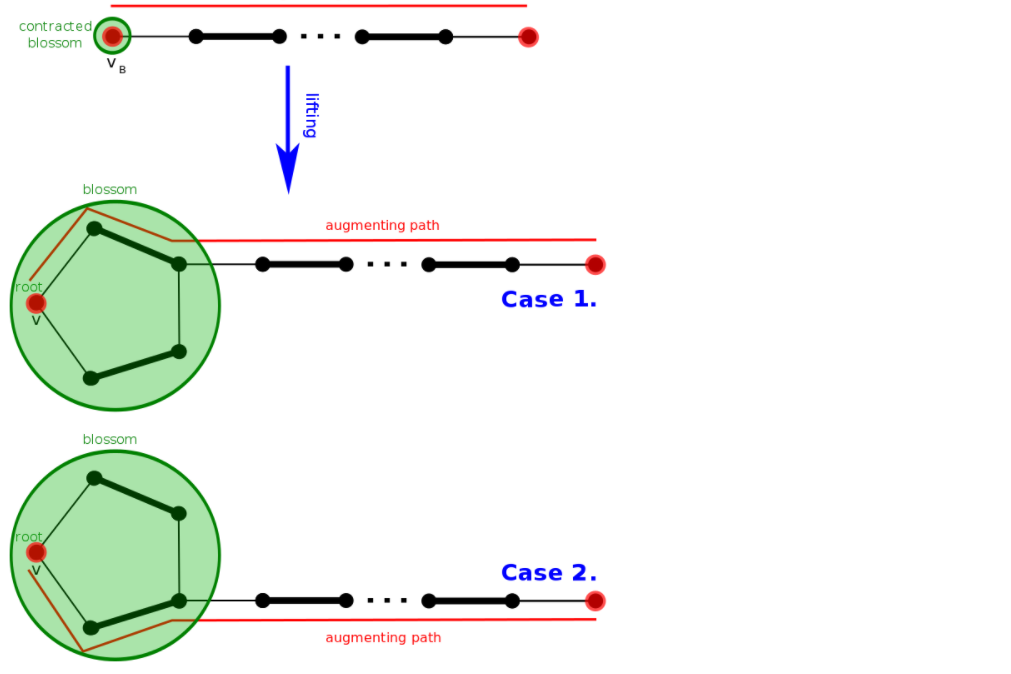
根據這個性質,可以將奇環縮成一個點(這個點稱為花),由於增廣路經過奇環,那么奇環內的增廣路可以還原出來,因此縮完點後的圖如果可以找到一條增廣路,那么原圖中也可以找到一條增廣路。
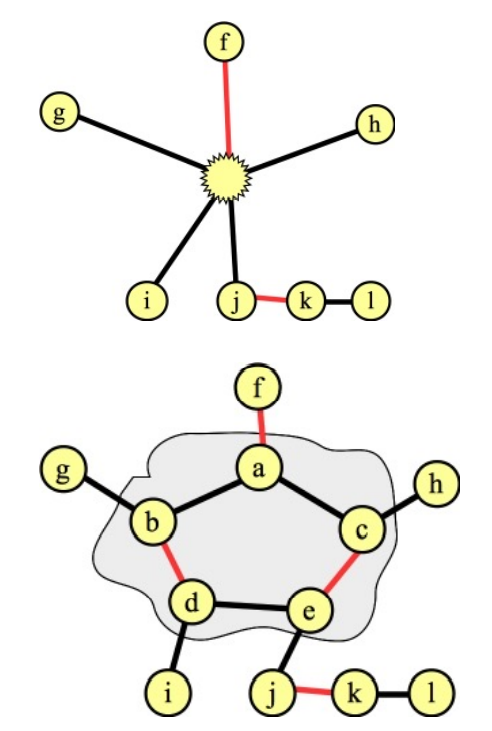
收縮示意圖