帶係數k的正規仿切觸黎曼流形((normal para-contact Riemannian manifold with a coefficient k)一類特殊的正規仿切觸流形.在一個n維殆仿切觸黎曼流形M中,若成立
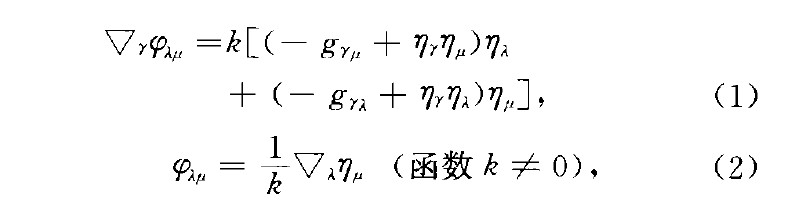
則M稱為帶有係數k的正規仿切觸黎曼流形,或稱M為帶有係數k的P佐佐木流形,又名EP佐佐木流形.k一1時,它就成為一個P佐佐木流形.在帶有係數k的P佐佐木流形中,曲率張量和結構向量滿足關係式:

容有單位撓形場的黎曼流形也是一個帶有係數k的P佐佐木流形.它的結構可稱為撓形結構,因此它也稱為具有撓形結構的殆仿切觸黎曼流形.設M是帶有係數k的P佐佐木流形.若它滿足
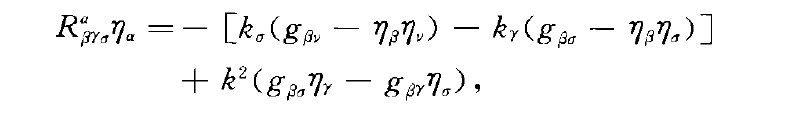
則它是較具撓形結構的殆仿切觸黎曼流形廣泛的一類EP佐佐木流形;而當滿足條件(3>時,則M是較具保圓型結構的仿切觸黎曼流形廣泛的一類EP佐佐木流形,且稱之為LP佐佐木流形.佐佐木流形和P佐佐木流形與其他流形一樣,從它引進以來便有豐富多彩的微分幾何與拓撲學的問題可供研究.有關的論述已由國內外許多學者所發表.特別是日本學者至今仍在對這些流形做不倦的研究,形形色色的各種結果在諸多雜誌上時有所見.
