帕克斯-麥克萊倫算法

帕克斯-麥克萊倫算法（英語：Parks–McClellan algorithm），為一個用以設計最佳化有限脈衝回響濾波器（finite impulse response filter）的疊代算法，由James McClellan and Thomas Parks於1972年的著作中提出。

此算法的主要精神，在於利用疊代的方式最小化濾波器在通帶(pass band)和止帶(stop band)的最大誤差，因此有時也稱為最小化最大誤差算法(Mini-max filter design)。由於帕克斯-麥克萊倫算法也屬於Remez-exchange algorithm為了設計有限脈衝回響濾波器而產生的一種變形，因此也有人以Remez-exchange algorithm代稱。

基本介紹

• 中文名：帕克斯-麥克萊倫算法
• 外文名：Parks–McClellan algorithm

有限脈衝回響濾波器設計

有限脈衝回響濾波器(finite impulse response filter)利用有限的點數來表示濾波器的脈衝回響，對於N點有限脈衝回響濾波器

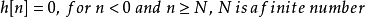
有限脈衝回響濾波器的優點在於脈衝回響是有限的，使得設計上較為簡單。然而如何在有限的點數下，設計出效果最近似於理想目標的濾波器，則是帕克斯-麥克萊倫算法所欲解決的問題。

對於濾波器設計，帕克斯-麥克萊倫算法的精神在於最小化最大誤差。在忽略通帶與止帶之間轉換帶(transition band)的情況下，最小化通帶與止帶的最大誤差：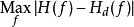

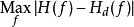
其中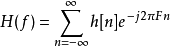 為設計濾波器的頻率回響，F為正規化頻率(normalized frequency)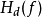， 則為理想目標濾波器的頻率回響。

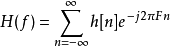
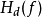
濾波器設計時，可利用weighting function將較重要的頻帶比重放大。如此一來，在利用帕克斯-麥克萊倫算法設計濾波器時，則會較重視比重較大頻帶的誤差。

若在加入weighting function情況下，可將帕克斯-麥克萊倫算法一般化。此時的最大誤差則可表示為：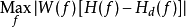

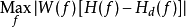
帕克斯-麥克萊倫算法

下面的文章將說明如何以該算法設計最佳化濾波器，假設

濾波器長度為N，且N為奇數可表示成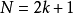

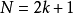
目標濾波器的頻率回響為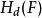 偶函式

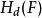
W(F)用以表示所指定的weighting function

此算法共分為6個步驟：

1、設定極值點起始值

在範圍的範圍內，任意選擇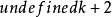 點頻率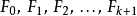 作為極值點(extreme frequency)的起始值。

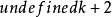
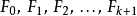
將此時的最大誤差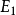 設為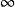 ，但所選擇的 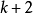點起始值不能落在轉換頻帶(transition band)，也不能將所有的起始直設在止帶(stop band)上。

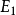
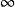
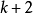
極端頻率為最後完成設計的濾波器頻率回響中，會出現最大誤差的頻率。一開始所給定的起始值是隨機的，會在此算法之後的步驟中逐漸收斂。

此時，令在各點極端頻率的誤差為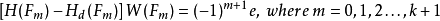

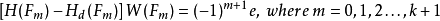
2、計算目前的頻率回響

為了方便算法運算之後的進行，我們可稍微整理誤差的表示方式。若令

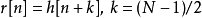
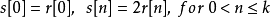
如此一來，可將在第1步驟中所得到的誤差式表示為：

其中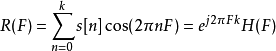， 經過整理之後可得

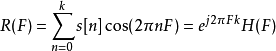
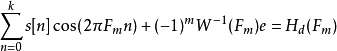
上述的誤差關係式，可表示為矩陣形式{\displaystyle Ax=H}

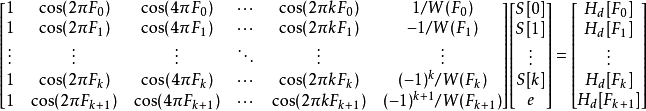
因此，我們可由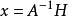計算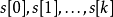

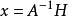
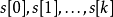
3、計算誤差函式

計算誤差函式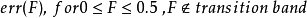

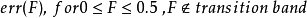
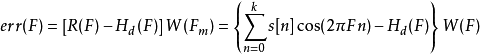
4、尋找極值點

從中，找k+2個區域極大或極小值，將區域極大或極小值出現的頻率標示為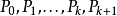

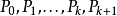
區域極大或極小值的判斷規則：

若找到多於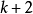個極值點，選擇極值點的優先順位為：

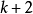
不是在邊界處的區域高峰(peaks)或低谷(dips)。在此，邊界區域即為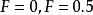以及頻率轉換帶的兩邊。

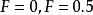
對於在邊界區域的頻率點，可用下列的標準判斷是否為區域極大或極小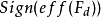：及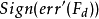為同相時，右邊界是極值點；反相時，左邊界是極值點；其他情況非極值點。

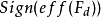
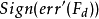
優先選擇不在邊界的極值點。

其次選在邊界的極值點中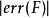，較大的，直到湊足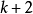個極值點為止。

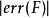
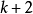
當邊界的極值點的一樣大時，優先選擇轉換頻帶兩旁的點。