基本介紹
- 中文名：布朗橋
- 外文名：Brown bridge
- 意義：連續時間的隨機過程
- 原理：維納過程W(t) 的條件機率分布
- 條件：B(0) = B(1) = 0
- 易錯點：非布朗運動
布朗橋定義,易錯分析,分析理解,布朗橋和經驗分布函式,布朗橋過程,定義,分類,
布朗橋定義
{B（t），
}為標準布朗運動，不妨B（0）=0，令
，則稱{
}為布朗橋。
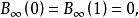
期望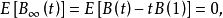
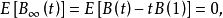
方差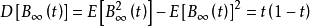
。
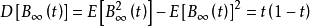
易錯分析
標準布朗橋是機率論中常見的一個研究對象。它是一種連續時間上的隨機過程，在0和1處取值為0.
注意不要和布朗運動混淆。
注意不要和布朗運動混淆。
布朗橋有時又被稱為綁在0和1處的布朗運動（此處僅為意譯）。
分析理解
了解布朗橋，先要知道布朗運動：懸浮微粒永不停息地做無規則運動的現象叫做布朗運動（布朗運動它不是固體分子的運動，不是液體分子的運動。它是固體微粒的運動，它是液體分子無規則運動的表現。），布朗運動可以定義為：B（t），t≥0。
為標準布朗運動，其中B（t）是連續時間的隨機過程。
方差為t（1−t）的時候橋的期望值是零，意思是最高不確定在橋中央，而在叉點處為零不確定；B（s）與B（t）的協方差是s（1−t）ifs<t，布朗橋的增長是非獨立性的。
如果W（t）是個標準的維納過程，B（t）=W（t）−tW（1）就是一個布朗橋。
如果相反，B（t）是個布朗橋，Z是個標準的隨機變數，那么W（t）=B（t）+tZ是t∈[0，1]區間的一個維納過程。
註：維納過程是一個重要的獨立增量過程。
布朗橋和經驗分布函式
在統計中，為了估量參量的統計特性，常常獨立的抽取樣本。
設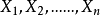
，獨立同分布，
，記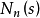
表示n個X中取值不超過s的個數：
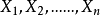
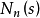
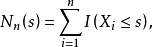
經驗分布函式：
記：
當
時，
正是布朗橋。
布朗橋過程
定義
布朗橋過程在研究經驗分布函式和經濟數學中有著大量的套用，布朗橋過程定義如下：
定義1：滿足下面隨機微分方程的解{x（t）}是一個布朗橋過程：Vost<T有dx（￡）：d￡+d（￡），式中W（t）是一個標準布朗運動。布朗橋過程與一 個布朗運動W（t）密切相關.布朗運動定義如下：
定義2：隨機過程{w（t）}如果滿足：1）W（0）=0；2）{w（t），t>0} 有獨立的平穩增量；3）對每個t≥0，W（t）服從常態分配N（0，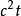
），則{w（t）}稱為標準布朗運動。
分類
自由布朗橋過程：當布朗橋過程樣本的跳躍點完全隨機決定時，把這種布 朗橋過程定義為自由布朗橋過程。
有約束布朗橋過程：有約束布朗橋過程是對自由布朗橋過程樣本函式進行約束的隨機過程，約束條件為特定傳播環境的幾何描述，使得每次射線發生反射的點都在障礙物的表面……例如在一個室內環境或與室內環境相近的環境中，房間的6個面，以及各個障礙物的表面，都是能夠使光線發生反射，散射或繞射作用的面。在無線信道的傳播環境中，存在特殊分布的散射體時，可用該過程對經過i次反射過程的電磁波進行建模。自由布朗橋過程中的布朗橋樣本，如果同時滿足以下三個條件，即為約束布朗橋過程的樣本：
