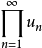基本介紹
- 中文名:布拉施克乘積
- 外文名:Blaschke product
- 適用範圍:數理科學
簡介,共形變換,無窮乘積,
簡介
若an(n=1,2,…)是一複數序列,0<|an|<1,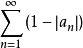 收斂,則無窮乘積
收斂,則無窮乘積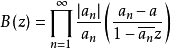 在|z|<1內收斂,B(z)稱為布拉施克乘積。
在|z|<1內收斂,B(z)稱為布拉施克乘積。
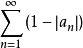
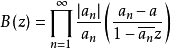
共形變換
共形變換是指一個曲面到另一個曲面的映射,如果處處保持微小區域的相似性,則叫做共形變換。
把平面當成複數域,則任何解析函式都是平面到平面的共形變換,而平面到平面的任何共形變換有似乎都能和一個解析函式相對應。當然共形變換不僅可以是平面到平面的變換,也可以是平面到曲面的變換或者曲面間的變換。
無窮乘積
(infinite product)
無窮乘積是把無窮序列的各項用乘號連結得到的表達式。
設{un}為一序列,u1u2...un…或記為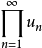 稱為無窮乘積。
稱為無窮乘積。