布利薩德算法(Blissard's calculus)亦稱啞運算,是一種特殊的符號演算法,它是英國數學家布利薩德(J.Blissard)創造的。
基本介紹
- 中文名:布利薩德算法
- 外文名:Blissard's calculus
- 別稱:啞運算
- 簡介:一種特殊的符號演算法
- 提出者:布利薩德(J.Blissard)
基本介紹,相關分析,
基本介紹
設數列{ak},{bk},{ck}(k=0,1,2…)的指數型生成函式分別為
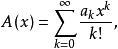
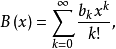
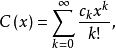
若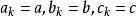 ,則
,則 ,按此算出結果後,再將相應指數移到下標位置,可以得出問題的真實答案,例如,將該算法用於指數型生成函式之積,若
,按此算出結果後,再將相應指數移到下標位置,可以得出問題的真實答案,例如,將該算法用於指數型生成函式之積,若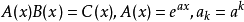 ,
,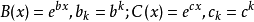 ,則
,則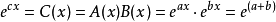 ,從而
,從而 ,由此得出
,由此得出
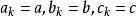

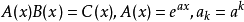
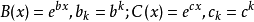
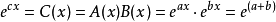

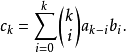
相關分析
指數型發生函式不僅對研究排列問題是必要的,而且在計算機率統計中的矩量時也是極有用的工具,這裡我們專來討論指數型發生函式的運算性質,特別要介紹Blissard形式演算法則。
令數列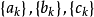 相應的指數型發生函式分別記作
相應的指數型發生函式分別記作
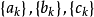
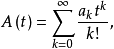
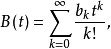
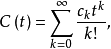
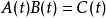
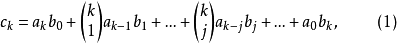

這就是說,在演算過程中可把足標移到指數地位來演算,但演算完畢之後,對最終結果仍須讓指數返回足標位置,這種形式算法即稱為Blissard演算或“啞演算”(umbral oalculas).
上述啞演算的合理性本質上是基於指數型發生函式在作乘法運算與求導等演算時,能與啞演算法則一一對應起來,並使最終結果具有一致性,具體說來,按啞演算規定法則,可簡記
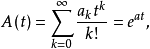
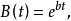
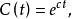
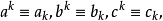
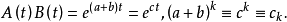
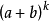
對A(t)進行求導運算,可得
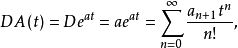
這表明啞演算仍繼續得出正確結果.由上所論,至少已能看出,啞演算套用於形式指函式的乘法與求導,總是行之有效的,當然,乘法與求導運算可以反覆進行。

