左高樹

左高樹是一棵二叉樹，且如果該二叉樹不空，則對其中的每個內部結點x，都有左兒子到一個外部結點的最短路程長度大於或等於右兒子到一個外部結點的最短路程長度。

基本介紹

• 中文名：左高樹
• 外文名：Leftist Trees
• 實質：擴充二叉樹
• 操作：合併操作
• 複雜度：O(logn)
• 套用學科：計算機科學

左高樹定義

設x是擴充二叉樹的一個結點，並令left_child(x)和right_child(x)分別表示內部結點的左、右兒子。定義shortest(x)為從x到一個外部結點的最短路程長度。

左高樹是一棵二叉樹，且如果該二叉樹不空，則對其中的每個內部結點x，都有：

Shortest(left_child(x))>= Shortest(right_child(x))。

左高樹的一個套用是合併操作，套用場景是:當某個優先佇列的伺服器關閉時,就需要將其與另一個正在運行伺服器的優先佇列合併。如果兩個佇列的元素總數為n，則一般的堆結構的複雜度為O(n),但是左高樹可以達到O(logn)。插入和刪除操作都可以通過合併操作來完成。

研究背景

堆結構是一種隱式數據結構（implicit data structure），用完全二叉樹表示的堆在數組中是隱式存貯的（即沒有明確的指針或其他數據能夠重構這種結構）。由於沒有存貯結構信息，這種描述方法空間利用率很高，事實上沒有空間浪費。儘管堆結構的時間和空間效率都很高，但它不適合於所有優先佇列的套用，尤其是當需要合併兩個優先佇列或多個長度不同的佇列時。因此需要藉助於其他數據結構來實現這類套用，左高樹（leftist tree）就能滿足這種要求。

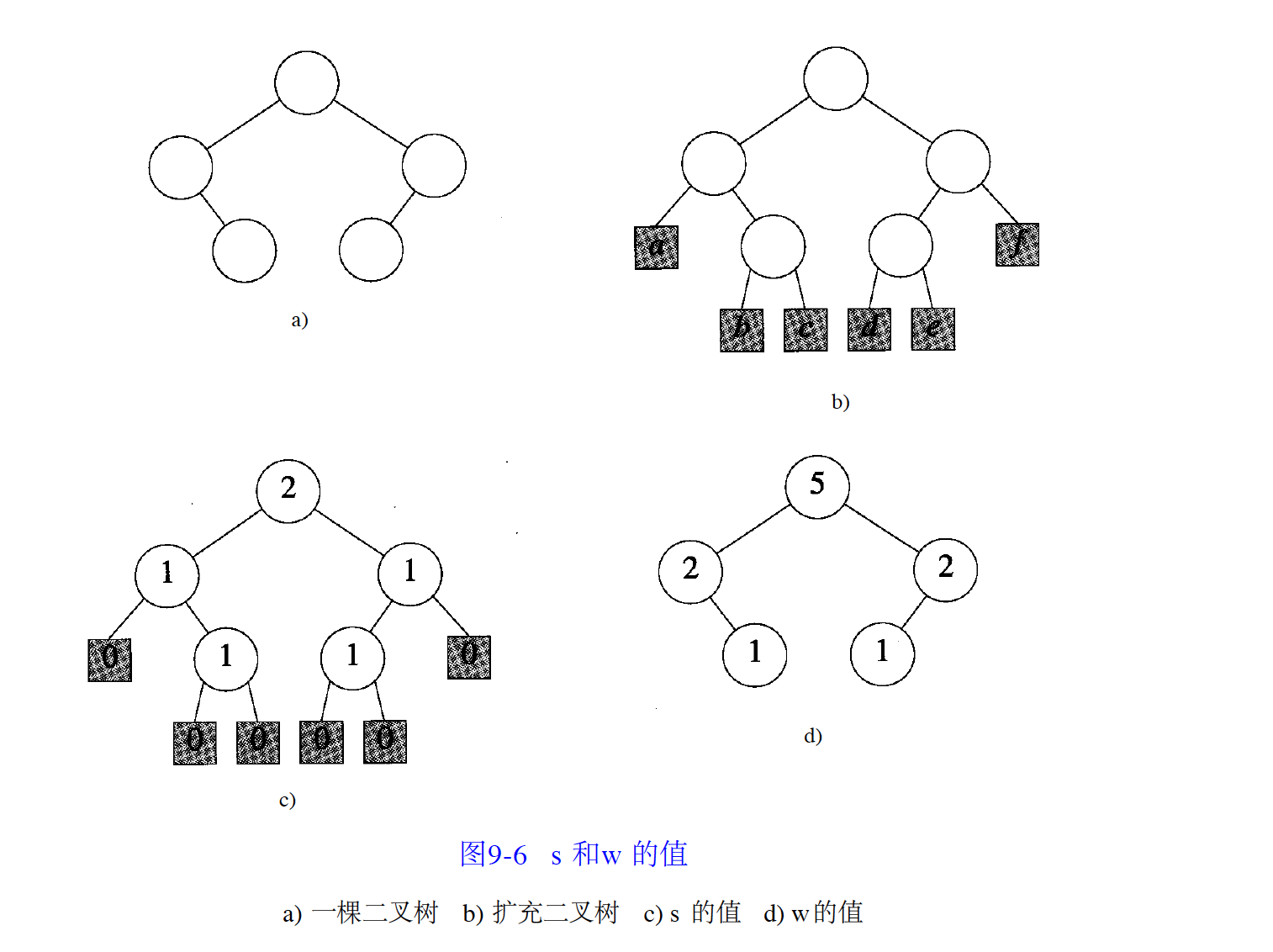
令s (x)為從節點x到它的子樹的外部節點的所有路徑中最短的一條，根據s(x)的定義可知，

若x是外部節點，則s的值為0，若x為內部節點，則它的s值是：

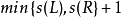
其中L與R分別為x的左右孩子。

最小左高樹

定義及操作

最小（最大）左高樹是一棵左高樹，其中的每個內部結點的關鍵字值不大於（不小於）該結點的兒子結點的關鍵字值。

對於最小左高樹的操作，插入和刪除最小元素操作都可以通過合併操作來完成。要把元素x插入到左高樹A中，先建立一棵只有一個元素x的最小左高樹B，再合併最小左高樹A和B。要從一棵非空最小左高樹A刪除最小元素，則只需合併最小左高樹A的左子樹和右子樹，再把最小左高樹的根結點刪除。

以下重點介紹最小左高樹的合併操作。

假設要合併最小左高樹A和B，首先，沿著A和B的最右路徑，得到一棵包含A和B所有元素的二叉樹（注意：這裡只是得到二叉樹，而不是最小左高樹）。使得該二叉樹具有以下性質：所有結點的關鍵字都不大於其兒子結點關鍵字。必要時交換結點的左、右子樹，將其轉化為最小左高樹。

合併操作

1、假設合併最小左高樹A和B，首先比較兩棵樹根結點的關鍵字值，以最小的關鍵字作為新二叉樹的根結點。

2、保留A的左子樹不變，將其右子樹與最小左高樹B合併，合併後的二叉樹成為新的A的右子樹。

3、把二叉樹轉換為最小左高樹從最後一個修改結點（注意：這裡不是最後結點）開始，回溯到最終的樹根結點，使得路徑上的所有結點滿足不等式：shortest（left_child()）>= shortest（right_child()）

高度優先左高樹

定義

若且唯若一棵二叉樹的任何一個內部節點，其左孩子的s值大於等於右孩子的s值時，該二叉樹為高度優先左高樹（height-biased leftist tree, HBLT）。

最大HBLT即同時又是最大樹的HBLT；

最小HBLT即同時又是最小樹的HBLT。

最大優先佇列可以用最大HBLT表示，最小優先佇列可用最小HBLT表示。可以通過考察子樹的節點數目而不是從根到外部節點的路徑來得到另一類左高樹。定義x的重量w(x)為以x為根的子樹的內部節點數目。注意到若x是外部節點，則其重量為0；若x為內部節點，其重量為其孩子節點的重量之和加1，圖中二叉樹各節點的重量如圖d所示。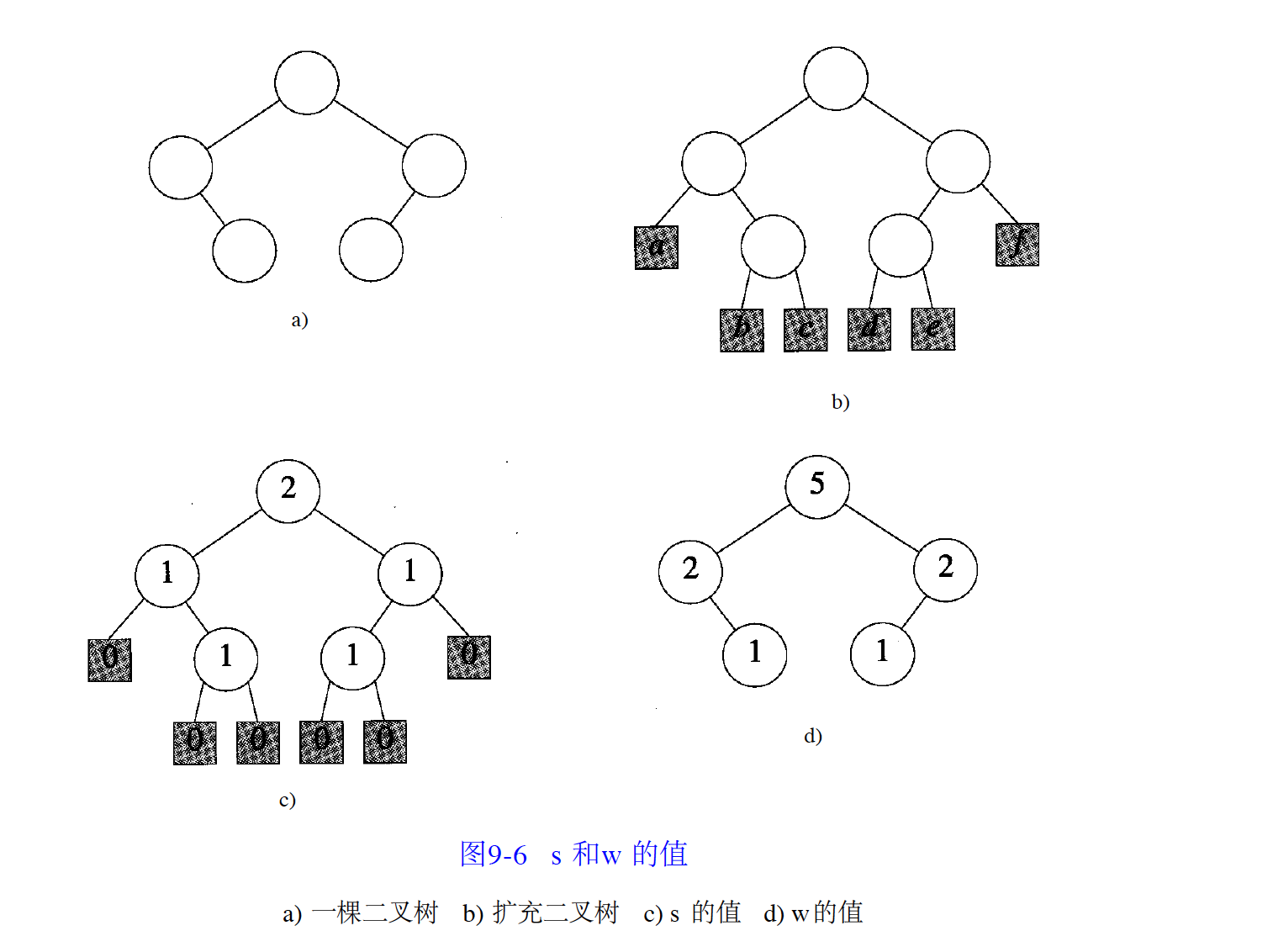

左高樹

定理

令x為一個HBLT的內部節點，則

1)以x為根的子樹的節點數目至少為2s (x)-1。

2)若子樹x有m個節點，s (x)最多為l o g2(m+ 1 )。

3)通過最右路徑（即，此路徑是從x開始沿右孩子移動）從x到達外部節點的路徑長度為s (x)。

證明：根據s (x)的定義可知，從x節點往下第s (x)-1層沒有外部節點（否則x的s值將更小）。

以x為根的子樹在當前層只有一個節點x，下一層有兩個，再下一層有四個，⋯⋯，x層往下第s (x)-1層有個2s (x) - 1，在s (x)-1層以下可能還有其他節點，因此子樹x的節點數目至少為i=s (x) - 12i= 2s (x)-1。

從1)可以推出2）。

根據s的定義以及HBLT一個節點的左孩子的s值總是大於等於其右孩子的s值，可以推得3）成立。

重量優先左高樹

若且唯若一棵二叉樹的任何一個內部節點，其左孩子的w值大於等於右孩子的w值時，該二叉樹為重量優先左高樹（weight-biased leftist tree, WBLT）；最大（小）WBLT 即同時又是最大（小）樹的WBLT。

同HBLT類似，具有m個節點的WBLT的最右路徑長度最多為log2(m+ 1 )。可以對WBLT與HBLT執行優先佇列的查找、插入、刪除操作，其時間複雜性與堆的相應操作相同。同堆一樣，WBLT與HBLT可線上性時間內完成初始化。用WBLT或HBLT描述的兩個優先佇列可在對數時間內合併為一個，而當用堆描述優先佇列時，則不能在對數時間內完成合併。