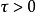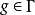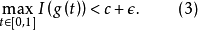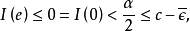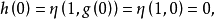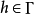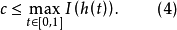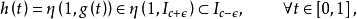山路引理(mountain pass lemma)是證明非線性橢圓型方程邊值問題有解的重要工具,是極小極大原理的一個簡單而重要的特殊情形,由義大利數學家阿姆布羅塞蒂(A.Am-brosetti , )和美國數學家拉比諾維茨(P. H.Rabi-nowitz)於1973年證明的定理。
基本介紹
- 中文名:山路引理
- 外文名:mountain pass lemma
- 所屬學科:數學
- 套用:微分方程邊值問題
- 提出者:阿姆布羅塞蒂,拉比諾維茨
定義,山路引理的證明,形變定理,引理,證明過程,
定義
山路引理設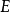 是Banach空間,
是Banach空間,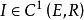 滿足
滿足
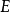
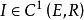
(i)  ,存在
,存在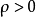 使得
使得 ;
;

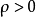

(ii) 存在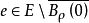 使得
使得 。
。
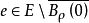

令 是
是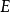 中聯結0與e的道路的集合,即
中聯結0與e的道路的集合,即

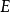
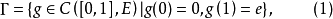
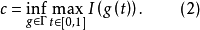
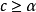



山路引理的證明
形變定理
設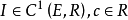 ,c∈R。如果
,c∈R。如果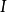 關於c沒有臨界序列,則存在
關於c沒有臨界序列,則存在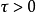 ,使得:對任意
,使得:對任意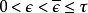 ,存在滿足下列條件的函式
,存在滿足下列條件的函式 :
:
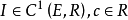
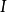
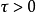
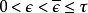

1°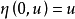 ;
;
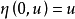
2°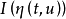 關於t是單調減函式,特別地有
關於t是單調減函式,特別地有
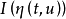
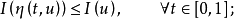
3° 當
當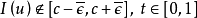 ;
;

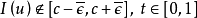
4° 是
是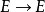 的同胚(對任意取定的
的同胚(對任意取定的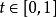 );
);

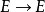
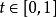
5°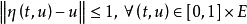 ;
;
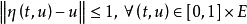
6°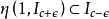 ;
;
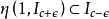
7°如果 為偶泛函,則
為偶泛函,則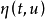 對u為奇運算元(t取定時)。
對u為奇運算元(t取定時)。

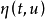
引理
設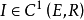 ,如果
,如果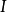 滿足P-S條件,且
滿足P-S條件,且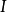 關於c有臨界序列,則c為
關於c有臨界序列,則c為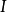 的臨界值。
的臨界值。
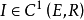
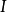
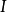
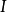
證明過程
證明: 任取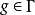 ,由於
,由於 連續,因而
連續,因而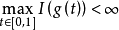 , 再由(2)知
, 再由(2)知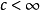 ,又對任意
,又對任意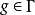 ,由條件(ii)及(i)有
,由條件(ii)及(i)有
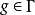

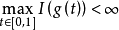
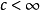
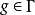
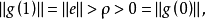
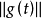
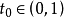


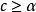
假如 關於c沒有臨界序列,由形變定理,存在
關於c沒有臨界序列,由形變定理,存在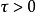 ,當
,當 時,存在
時,存在 具有性質1°~6°。對
具有性質1°~6°。對 ,由(2)知道:存在
,由(2)知道:存在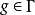 使得
使得