按照博克里斯和馬修斯的觀點,對稱因子是一個控制電能向化學能轉換的係數。與此相似的是多戈納澤提出的概念,他認為對稱因子是金屬中一個軌道被占據的幾率的度量。
基本介紹
- 中文名:對稱因子
- 外文名:symmetry factor
- 類型:物理量
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:電能向化學能的轉換
概念,對稱因子隨電位的變化,
概念
係數 就稱為對稱因子,其值接近1/2,但正、逆反應的
就稱為對稱因子,其值接近1/2,但正、逆反應的 值可有所不同。
值可有所不同。 與位能-距離分布圖中反應物和產物所在點的梯度有關。如果靠近交點的斜率對產物為
與位能-距離分布圖中反應物和產物所在點的梯度有關。如果靠近交點的斜率對產物為 、對反應物為
、對反應物為 ,則
,則





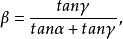
對稱因子隨電位的變化
為了確定對稱因子對電位的影響,有必要在更負的電位下工作,此時電位對勢壘形狀的影響是顯著的。這項工作在1960年是首先由德斯皮克和博克里斯完成的。他們為了確定上述影響,選擇了銀沉澱反應,並且通過在高過電位和非常短時間下工作,避免了遷移的影響,從而得以畫出考慮對稱因子 隨過電位η而變化的
隨過電位η而變化的 曲線圖(如圖1)。
曲線圖(如圖1)。


 圖1
圖1對稱因子 藉助莫爾斯參數隨過電位η而變化的理論同近代某些人所採用的非諧性較正方法相比,是一種更普遍的理論方法。按照德斯皮克和博克里斯的作法,方程可推導如下。
藉助莫爾斯參數隨過電位η而變化的理論同近代某些人所採用的非諧性較正方法相比,是一種更普遍的理論方法。按照德斯皮克和博克里斯的作法,方程可推導如下。

分別為溶劑化離子和吸附離子所固有的曲線AA和BB(如圖2)可用方程表示:
 圖2
圖2




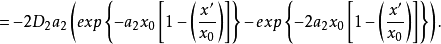
根據上面兩個方程,可得:

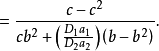
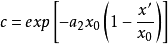






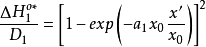
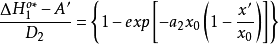
關於對稱因子 隨電位而變化的其他工作一直是有限的,帕森斯和帕瑟朗的工作是按連續介質的靜電近似來解釋的,然而,根據這種解釋,其
隨電位而變化的其他工作一直是有限的,帕森斯和帕瑟朗的工作是按連續介質的靜電近似來解釋的,然而,根據這種解釋,其 值理應隨過電位而連續變化。
值理應隨過電位而連續變化。





