對稱分量法（method of symmetrical components）是電工中分析對稱系統不對稱運行狀態的一種基本方法。廣泛套用於三相交流系統參數對稱、運行工況不對稱的電氣量計算。
基本介紹
- 中文名：對稱分量法
- 外文名：method of symmetrical components
- 所屬學科：物理
- 範圍：電學
- 發明者：Charles LeGeyt Fortescue
- 發明時間：1918年
簡介,原理,
簡介
電力系統正常運行時可認為是對稱的，即各元件三相阻抗相同，各自三相電壓、電流大小相等，具有正常相序。電力系統正常運行方式的破壞主要與不對稱故障或者斷路器的不對稱操作有關。由於整個電力系統中只有個別點是三相阻抗不相等，所以一般不使用直接求解複雜的三相不對稱電路的方法，而採用更簡單的對稱分量法進行分析。
電力系統正常運行時可認為是三相對稱的，即各元件三相阻抗相同，三相電壓、電流大小相等，相與相間的相位差也相等，且具有正弦波形和正常相序。對稱的三相交流系統，可以用單相電路來計算。只要計算出一相的量值，其他兩相就可以推算出來，因為其他兩相的模值與所計算相相等，相位相差正負120度。三相對稱短路或斷線時，交流分量三相是對稱的。因此，可以利用系統固有的對稱性，只需分析其中一相，避免逐相進行計算的複雜性。
但是，電力系統發生單相接地短路、兩相短路和兩相接地短路，以及單相斷線和兩相斷線等不對稱故障時，三相阻抗不相同，三相電壓、電流大小不相等，相與相間的相位差也不相等。對這樣的三相系統不能只分析其中一相，通常採用對稱分量法進行分析。
但是，電力系統發生單相接地短路、兩相短路和兩相接地短路，以及單相斷線和兩相斷線等不對稱故障時，三相阻抗不相同，三相電壓、電流大小不相等，相與相間的相位差也不相等。對這樣的三相系統不能只分析其中一相，通常採用對稱分量法進行分析。
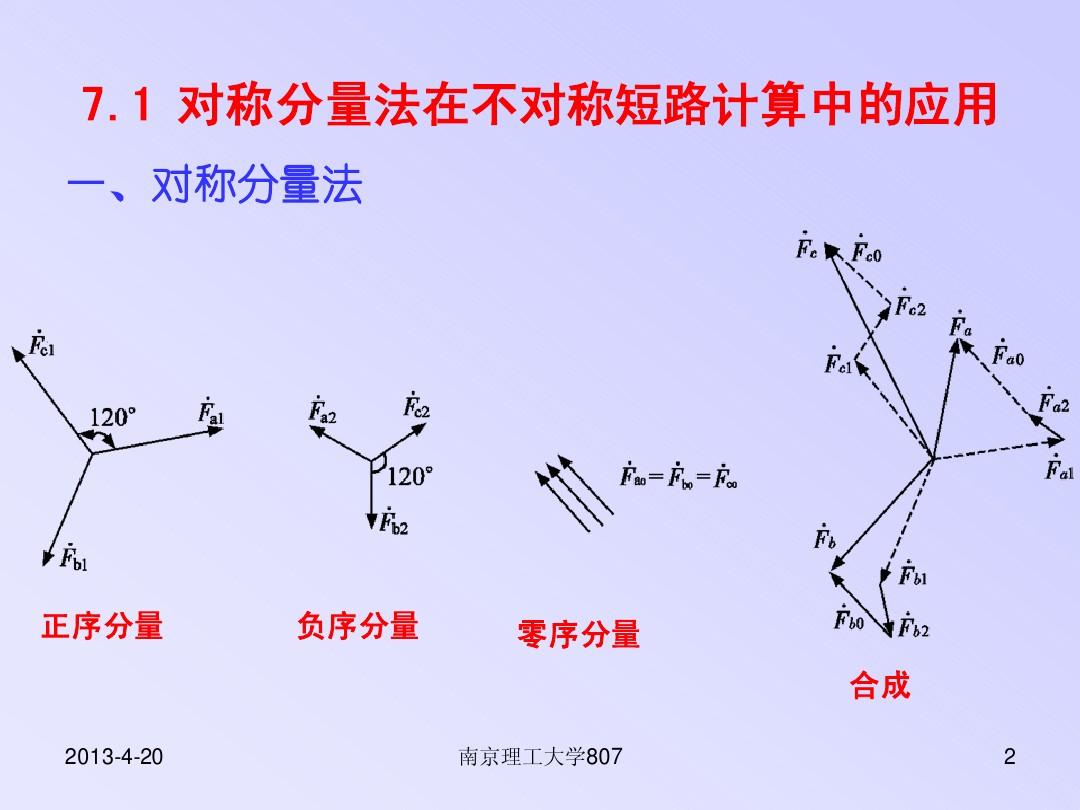
對稱分量法是電力系統短路電流計算的基本方法，其目的是將一組不對稱的ABC量，變換為三組各自對稱的三相相量，分別稱為正序、負序和零序量。與各序電壓、電流量對應，電力系統也分為正序、負序和零序網路。
電力系統發生不對稱故障後產生的不對稱電壓、電流量，通過套用對稱分量法，可以將其分解到三個序網，在各序網內按照序電壓、電流對稱的方式進行分析，之後再合成為實際的ABC量，從而使得不對稱故障計算大為簡化。
電力系統發生不對稱故障後產生的不對稱電壓、電流量，通過套用對稱分量法，可以將其分解到三個序網，在各序網內按照序電壓、電流對稱的方式進行分析，之後再合成為實際的ABC量，從而使得不對稱故障計算大為簡化。
對稱分量法（method of symmetrical components）由加拿大電氣學家Charles LeGeyt Fortescue發明於1918年。
原理
電工中分析對稱系統不對稱運行狀態的一種基本方法。電力系統中的發電機、變壓器、電抗器、電動機等都是三相對稱元件，經過充分換位的輸電線基本上也是三相對稱的。對於這種三相對稱系統的分析計算可以方便地用單相電路的方法求解。任何不對稱的三相相量 A，B，C 可以分解為三組相序不同的對稱分量：①正序分量A1，B1，C1，②負序分量A2，B2，C2，③零序分量A0，B0，C0。即存在如下關係：
對稱分量法
對稱分量法V0=UA0=UB0=UC0
V1=UA1=aUB1=a2Uc1
V2=UA2=a2UB2=aUC2
其中
，定義是單位相量"i"依逆時針方向旋轉120度。
在計算電力系統不平衡情況下引用了對稱分量法，即任何三相不平衡的電流、電壓或阻抗都可以分解成為平衡的相量成分即正相序（UA1、UB1、UC1）、負相序（UA2、UB2、UC2）和同向的零相序（UA0、UB0、UC0），即有：UA=UA1+UA2+UA0，UB=UB1+UB2+UB0，UC=UC1+UC2+UC0，其正相序的相序（順時方向）依次為UA1、UB1、UC1，大小相等，互隔120度；負相序的相序（逆時方向）依次為UA2、UB2、UC2，大小相等，互隔120度；零相序大小相等且同相，各相序都是按逆時針方向旋轉。在對稱分量法中引用運算元a，其定義是單位相量依逆時針方向旋轉120度，則有：UA0=1/3（UA+UB+UC），UA1=1/3（UA+aUB+a2UC），UA2=1/3（UA+a2UB+aUC）注意以上都是以A相為基準，都是矢量計算。知道了UA0實際也知道了UB0和UC0，同樣知道了UA1也就知道了UB1和UC1，知道了UA2也就知道了UB2和UC2。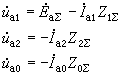
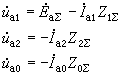對稱分量法
對稱分量法
對稱分量法對稱分量法