利用廣義線性模型解決二分類任務的一種方法。
基本介紹
- 中文名：對數幾率回歸
- 外文名：logistic regression或logit regression
定義,性質,套用,
對數幾率回歸，簡稱對率回歸，又稱邏輯回歸，是使用Sigmoid函式作為聯繫函式時的廣義線性模型，是廣義線性模型的一個特例。
定義
假設要用列向量
預測二分類結果
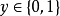，有數據集
。
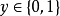
由廣義線性模型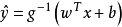
可知，只要找一個聯繫函式
，其值域為
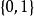即可。
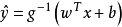
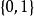
最理想的聯繫函式是單位階躍函式（unit-step function）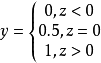
。
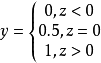
但是單位階躍函式不連續，難以求導，所以用對數幾率函式代替。
對數幾率函式（logistic function），簡稱對率函式，定義式為
。
得到擬合模型
。
為簡便起見，設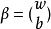
，
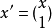，則有
。
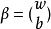
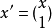
下面將擬合模型的因變數看作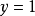
的機率，使用極大似然法。
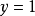
對於數據集的每一個樣本，有機率
。
考慮到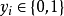
，則有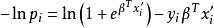
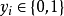
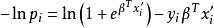
求出令損失函式
最小時的
值，就可求出模型參數。
性質
可使用梯度下降法、牛頓法等求損失函式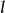
最小時的
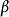參數值。
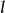
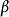
套用
二分類任務
