單點可以構成無數條射線，且其中一條射線上的點可以構成L=1/2（A^2-A）條線段。
基本介紹
- 中文名：射線定理
- 類型：數學定理
- 學科：數學
- 特點：只有一個端點，另一邊可無限延長
射線,射線定理,射線定理解析幾何,射線定理與運動,射線定理與質點量,
射線
在幾何光學中，射線是描述光線或其他電磁輻射傳播的方向的一條曲線。這種射線和物理光學的波前垂直。
在大部分的簡單情況，在給定的傳導體內的光射線是直線。光線經過一個傳導體到另一個傳導體，其路徑符合司乃耳定律的折射或全內部反射。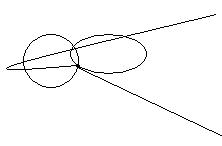
直射線、曲射線、回歸射線
直射線、曲射線、回歸射線特點
（1）只有一個端點，另一邊可無限延長。
（2）不可測量。
射線定理
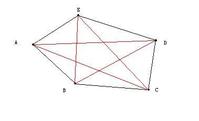
例：平面內任意5個點所組成的圖形（如右圖）由多少條線段構成？
已知A=5 L=1/2（A^2-A)=1/2×（25﹣5）=10a
即為平面內點所構成的最大線段數。
線段
線段是兩點間的一段連線，連線可以是曲線也可以是直線。
兩點之間可以有無數條線段，其中一條最短線段稱為直線段。
射線定理解析幾何
點密度
定義：距離間所含的點的個數與該距離的長度的比值。
定義式：Pa=A/X
單位：點每米a/m 點每厘米 a/cm
線密度
定義：距離間所含線段的條數與該距離的長度的比值。
定義式：Pi=L/X
單位：線段每米i/m 線段每厘米i/cm
點密度、線密度關係 兩條距離長度相等的線段，它們的點密度和線密度之比分別等於其點數及線段數之比。
Pa1 ：Pa2=A1 ：A2
Pi1 : Pi2=L1 ：L2
同一線段上的點密度與線密度之比等於其點數與線段數之比。
Pi : Pa=L : A
同一直線上的點密度與線密度的關係Pi=1/2(Pa^2-Pa)
距離式
推導：L=1/2（A^2-A）
PiX=1/2(Pa^2X^2-PaX)
X=2Pi+Pa/Pa^2
例：1.已知一個圓上有20個點，圓周長的線密度為1.9i/cm，求圓的點密度和圓的半徑？
解：據射線定理得L=1/2（A^2-A）=1/2(400-20)=190i
X= C=L/Pi=190/1.9cm=100cm
R=C/2π=100/ 6.283=15.91cm
2.已知某物體運動的一段軌跡，軌跡的點密度為3.1a/m，求這段軌跡的線密度和長度?
解：據射線定理得L=1/2（A^2-A）
同一軌跡上 Pa=3.1a/m Pi=1/2（A^2-A）=1/2(3.1^2-3.1)=3.225i/m
X=2Pi+Pa/Pa^2 =2×3.225/3.1^2=0.67m
射線定理與運動
勻速式
X=2Pi+Pa/Pa^2 X=vt
v=2Pi+Pa/Pa^2t
例：某小球勻速運動通過一點密度為2.11a/m的直線，所花時間為12s，求物體勻速運動的速度大小？
解：同一直線Pa=2.11a/m Pi=1/2(Pa^2-Pa)=1.17105/m
v=2Pi+Pa/Pa^2t=0.083m/s
力的Pi、Pa式
運動學公式V^2-V0^2=2aX 力的定義式F=ma
距離式X=2Pi+Pa/Pa^2
得F=Pa^2V^2m-Pa^2V0^2m/4Pi+2Pa
功的Pi、Pa式
功的定義式W=FX（a=90°）
F=Pa^2V^2m-Pa^2V0^2m/4Pi+2Pa
X=2Pi+Pa/Pa^2
W=FX=Pa^2V^2m-Pa^2V0^2m/2Pa^2
例：已知某質量為100kg的物體做勻加速直線運動的初末速度分別為3m/s和24m/s，位移的點密度為36.1a/m，求物體運動所受力的大小和物體運動所做的功？
解：同一位移上Pi : Pa=L : A
Pi=LPa/A=1/2（A^2-A）Pa/A=1/2(36.1^2-36.1)×36.1/36.1=636i/m
F=Pa^2V^2m-Pa^2V0^2m/4Pi+2Pa
=36.1^2×24^2×100-36.1^2×3^2×100/4×636+2×36.1
=28244.02N
X=2Pi+Pa/Pa^2=2×636+36.1/36.1^2=1m
W=FX=28244.02J
動線速
定義：某物體運動的速度與運動軌跡線密度的乘積。
定義式：Di=PiV
單位：線段每秒i/s
動點速 定義：某物體運動的速度與運動軌跡點密度的乘積。
定義式：Da=PaV
單位：點每秒a/s
例：1.小球以40m/s的速度通過一線密度為131.2i/m的直線，求動線速、動點速多大？
解：Di=PiV=40×131.2=5248i/s
131.2=1/2(A^2-A)
A=16.7或-15.71（舍）
Pa=APi/L=16.7×131.2/131.2=16.7a/s
Da=PaV=16.7×40=668a/s
2.已知地球繞太陽公轉一周的平均速度約為30km/s動點速為3.2×10^-8a/s，求太陽的質量？（G=6.67×10^-11N·m^2/s^2）
解：由題意得Da=3.2×10^-8a/s V=30000m/s
Pa=Da/V=3.2×10^-8/30000=1.06×10^-12a/m
∵地球繞太陽公轉視為一個為動點
Pa=A/X X=A/Pa=1/1.06×10^-12=9.4×10^11m
R=C/2π=9.4×10^11/2π=1.49×10^11m
據萬有引力、向心力公式得
M（日）=4π^2R^3/GT^2=4π^2×(1.49×10^11)^3/6.67×10^-11×(365×24×3600)=1.98×10^30kg
射線定理與質點量
質點量
mass point quantity
如果物體本身的大小和形狀對研究它的運動沒有影響或影響很小，我們就可以用一個有質量的點來代替整個物體，這個用來代替整個物體的與物體具有相同質量的點，叫做質點。據F=Pa^2V^2m-Pa^2V0^2m/4Pi+2Pa中Pa^2V^2m-Pa^2V0^2m是一個具有特殊意義的量，它描述了一個質點運動的質量和位移大小及初末位置的速度的變化情況，所以Pa^2V^2m我們定義為質點量。
定義：質點的動點速的平方與其質量的乘積
表達式：Q=Da^2V=Pa^2V^2m
單位：a^2·kg/s^2
例：1.一個質量為2kg小球以5m/s的速度從A地運動到B地，發生的位移為1000m，求這個小球的質點量大小？
解：Pa=A/X=2/1000=0.002a/m
Q=Pa^2V^2m=0.002^2×25×2=0.0002a^2·kg/s^2
2.一個質量為20kg的物體做初速度為零的勻加速直線運動，末速度為16m/s，通過位移150m，求這個過程中物體質點量的變化值大小？
解：Pa=A/X=2/150=0.013a/m
ΔQ=Pa^2V^2m-Pa^2V0^2m=0.013^2×16^2×20-0=0.887a^2·kg/s^2
