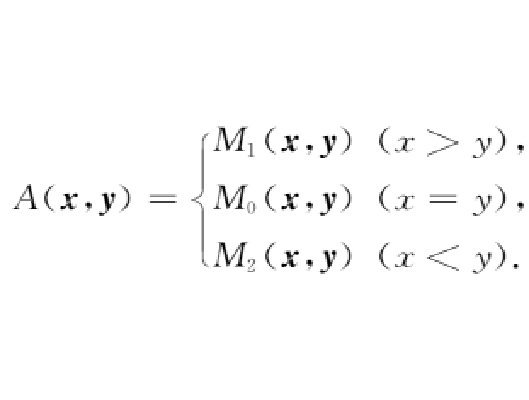定時對策(game of timing)是一類特殊的兩人無限零和對策,是單位正方形上的對策,局中人尋求純策略表達和採取行動的時間選擇。20世紀50年代,曾用這類對策解決了一些軍事問題,特別是建立了一些空軍戰略和空戰的模型,得出了一些有意義的結果。
基本介紹
- 中文名:定時對策
- 外文名:game of timing
- 所屬學科:數學
- 所屬問題:運籌學(對策論)
- 相關問題:支付函式,兩人零和對策等
基本介紹,相關概念與分析,
基本介紹
定義在單位正方形上的無限對策,如果它的支付函式取下列形式:
相關概念與分析
定時對策的典型例子是決鬥(duel)。假定有兩個決鬥者(局中人),每個局中人只有一粒子彈,在時間區間 中開槍。開槍時間越晚,離對手越近,命中率越高。但是,離對手越近,被對手擊中的可能性越大。因此,決鬥雙方都需選擇一個最優策略——適當的時機開槍。這個例子可以用來描述軍事戰爭,如決鬥者換成空戰雙方只攜帶一枚飛彈的戰鬥機;也可用來描述商業行動:如兩個占有同一市場的寡頭,雙方都想把對手擠出市場,用降低價格的方法進行傾銷。前者在第二次世界大戰中得到充分研究,後者在40 年代和50 年代也有過不少研究。下面給出這一類對策的數學模型。
中開槍。開槍時間越晚,離對手越近,命中率越高。但是,離對手越近,被對手擊中的可能性越大。因此,決鬥雙方都需選擇一個最優策略——適當的時機開槍。這個例子可以用來描述軍事戰爭,如決鬥者換成空戰雙方只攜帶一枚飛彈的戰鬥機;也可用來描述商業行動:如兩個占有同一市場的寡頭,雙方都想把對手擠出市場,用降低價格的方法進行傾銷。前者在第二次世界大戰中得到充分研究,後者在40 年代和50 年代也有過不少研究。下面給出這一類對策的數學模型。

以“無聲決鬥”(silent duel)為例。兩個局中人(決鬥者)在相距2 時同時面向而行,每個局中人在時間單位 中只開槍一次,它不知道對手是否被擊中,當局中人1在
中只開槍一次,它不知道對手是否被擊中,當局中人1在 處開槍,擊中對手的機率為
處開槍,擊中對手的機率為 ,局中人2在
,局中人2在 處開槍,擊中對手的機率為
處開槍,擊中對手的機率為 。
。





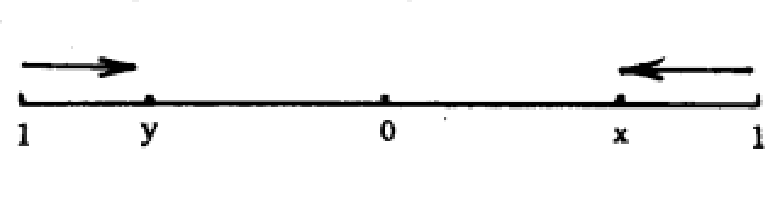 圖1
圖1設 是連續單調減函式(距離越遠,命中率越低),且
是連續單調減函式(距離越遠,命中率越低),且 。如果局中人1擊中對手而自己沒有損傷(對手沒開槍或者開槍沒有命中)嗎,其支付為1。
。如果局中人1擊中對手而自己沒有損傷(對手沒開槍或者開槍沒有命中)嗎,其支付為1。


如果局中人1被擊中,則支付為-1。如果雙方打成平手,即同時沒命中或同時命中,雙方的支付均為0。該對策的支付函式為




定義 設兩人零和對策的支付函式 有界,如果
有界,如果











定理設單位正方形上對策的支付函式為