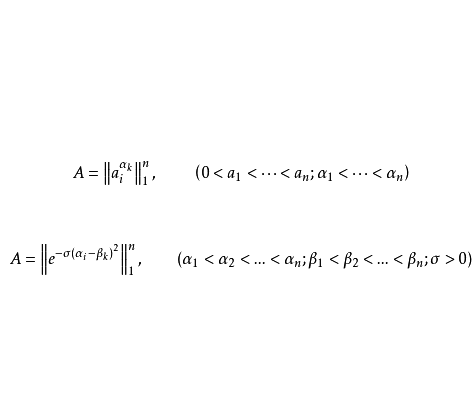完全正矩陣

完全正矩陣(totally positive matrix)是一個重要的非負矩陣子類，起源於穩定性理論的研究，在彈性系統之微振動理論等方面有廣泛的套用。若A=(a_ij)_n×n≥0滿足所有子式皆正(非負)，則稱A為完全正(非負)陣，記為A∈TP(TN)。若A∈TP，則下述基本結論成立：1.A∈P且每一特徵值皆為非負實數；2.若σ(A)={λ₁(A)≥λ₂(A)≥…≥λ_n(A)}，A_k為A划去k行k列後得到的n-1階子陣，則λ₁(A)≥λ₁(A_k)≥λ₂(A)，λ_n-1(A_k)≥λ_n(A)，1≤k≤n；3.det A≤det A_pdet A_n-p，式中A_p表示A之p階順序主子陣，A_n-p表示A之後n-p階主子陣。

基本介紹

• 中文名：完全正矩陣
• 外文名：totally positive matrix
• 起源：穩定性理論
• 所屬學科：數學
• 套用：彈性系統之微振動理論等方面

定義介紹

定義1矩陣稱為階符號確定矩陣，如果對任意的，所有異於零的p階子式有同樣的符號。如果這時對任意的，所有p階子式異於零，我們將稱矩陣A是d階嚴格符號確定矩陣.

特別地，在時，d階符號確定(嚴格符號確定)矩陣稱為d階完全非負(完全正)矩陣。

關於振盪矩陣的概念推廣如下：

定義2 階符號確定矩陣被稱為階矩陣，如果矩陣A 的某次冪是d階嚴格符號確定矩陣。

顯然，振盪矩陣是階完全非負矩陣。

附註:當時，我們去掉詞“d階”並簡單地說成符號確定矩陣、嚴格符號確定矩陣、完全非負矩陣、完全正矩陣。

定義3 矩陣將被稱為完全非負(完全正)的，如果它的所有任意階子式非負(為正)：

， （在時）

相關性質

我們指出完全非負矩陣的某些簡單性質：

① 兩個完全非負矩陣的乘積是完全非負矩陣。

② 完全正矩陣與非奇異的完全非負矩陣的乘積是完全正矩陣。

③ 如果非奇異矩陣A是完全非負的，那么它的逆矩陣是符號規則的；相反，如果一個非奇異矩陣A是符號規則的，那么它的逆矩陣是完全非負的。

④如果矩陣A是完全正的，那么它的逆矩陣是嚴格符號規則的；相反，如果一個矩陣A是嚴格符號規則的，那么它的逆矩陣是完全正的。

⑤如果非奇異矩陣A是完全非負的，那么矩陣也是完全非負的；如果矩陣A是完全正的，那么矩陣也是完全正的。

實例分析

例1所有完全非負矩陣(完全正矩陣)是符號確定(嚴格符號確定)矩陣。

例2如果在完全非負(完全正)矩陣A 中以相反的次序交換所有的行(或所有列)，那么得到符號確定(嚴格符號確定)矩陣。這時對任意的，將有

例3 雙元矩陣具有元素

這裡所有的數異於零，若且唯若所有數有同樣的符號，所有數有同樣的符號並滿足下列兩組不等式之一時是符號確定的：

① 或 ②

在情況①下，在情況②下，。

矩陣的秩r等於不等式①中小於號(相應的②中的大於號)的個數加1。

這個結論的正確性由任意階雙元矩陣的子式由數表出的公式推出。

例4 廣義范德蒙特矩陣

是完全正矩陣。

例5矩陣

是完全正矩陣。