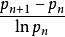基本介紹
- 中文名：孿生質數
- 外文名：Twin prime
- 別稱：孿生素數
- 套用學科：數學
- 適用領域範圍：數論
- 核心問題：孿生素數猜想
- 定義：兩個相差為2的素數
質數簡介,發展史,孿生素數無限多的證明,陰性合數定理和陰性素數定理,陽性合數定理和陽性素數定理,與孿生素數相對應的完全不等數,誤差分析,總結,最大值,非估算性,估算性,其他方式,
質數簡介
素數是指正因數只有1和本身即只能被自身和1整除的正整數，“孿生素數”則是指兩個相差為2的素數，例如3和5，17和19等。而隨著素數的增大，下一個素數離上一個素數應該越來越遠，故古希臘數學家歐幾里得猜想，存在無窮多對素數，他們只相差2，例如3和5，5和7，2003663613×2195,000-1和2003663613×2195,000+1等等。
1849年，波林那克（Alphonse de Polignac）提出了更一般的猜想：對所有自然數k，存在無窮多個素數對 (p,p + 2k)。k= 1的情況就是孿生素數猜想。
發展史
素數——那些因數除了1就是他們本身的數。從歐幾里得——他在2000年前證明了素數有無窮多個後，它就讓無數數學家為之傾倒。
因為素數從根本上和乘法相關，理解他們和加法相關的性質就變得很困難。一些數學上最古老的未解之謎就和素數和加法相關，其中之一就是孿生素數猜想——存在無 限多組差為2的素數對。另一個則是哥德巴赫猜想，這個猜想提出所有的偶數都可以表示為兩個素數之和。
在自然數列的起始部分存在著大量的素數，但是 隨著數字變大，它們變得越來越稀少。舉例來說，在前10個自然數裡，40%都是素數——2，3，5和7——但是在所有的10位數里，僅有4%的數是素數。 在過去的一個世紀裡，數學家們掌握了素數減少的規律：在大數中，連個素數之間的間隔大約是位數的2.3倍。舉例說明，在100位的數中，兩個素數的平均間 隔大約是230。
但是這只是平均而言。素數通常比平均預計的更加緊密的出現，或者相隔更遠。具體來說，“孿生”素數通常扎堆出現，比如3和 5還有11和13，他們的差僅為2。而在大數中，孿生素數似乎從沒有完全消失（詳見本詞條的最大值）。
1849年，法國數學家阿爾方·波利尼亞克提出了“波利尼亞克猜想”：對所有自然數k，存在無窮多個素數對(p,p+2k)。k等於1時就是孿生素數猜想，而k等於其他自然數時就稱為弱孿生素數猜想（即孿生素數猜想的弱化版）。因此，有人把波利尼亞克作為孿生素數猜想的提出者。
從那時開始，這些猜想的內在吸引力冠予了它們數學的聖杯的稱號，雖然他們可能沒有實際的套用價值。雖然有很多數學家們致力於證明這一猜想，他們還是不能排除素數的間隔會一直增長最終超過一個特定上限的可能。
1921年，英國數學家戈弗雷·哈代和約翰·李特爾伍德提出一個與波利尼亞克猜想類似的猜想，通常稱為“哈代-李特爾伍德猜想”或“強孿生素數猜想”（即孿生素數猜想的強化版）。這一猜想不僅提出孿生素數有無窮多對，而且還給出其漸近分布形式。中國數學家周海中指出：要證明強孿生素數猜想，人們仍要面對許多巨大的困難。
孿生素數無限多的證明
關鍵字:完全不等數,SN區間,LN區間，對應數段。.
陰性合數定理和陰性素數定理
大於3的素數隻分布在6n-1和6n+1兩數列中。（n非0自然數，下同）
6n-1數列中的合數叫陰性合數，其中的素數叫陰性素數（q)。
6[6NM+（M-N）]-1=（6N+1）（6M-1）（N M兩個非0自然數，N=〈 M，下同）
6乘以陰性上等數減去1等於陰性上合數。
6[6NM-（M-N）]-1=（6N-1）（6M+1）
6乘以陰性下等數減去1等於陰性下合數。
在6n-1數列中只有這兩種合數，餘下就是陰性素數了，所以就有陰性素數定理
x=/=6NM+-（M-N）
陰性不等數不等於陰性上下兩式。
6x-1=q
6乘以陰性不等數減去1等於陰性素數。
陽性合數定理和陽性素數定理
6n+1數列中的合數叫陽性合數，其中的素數叫陽性素數(P)。
6[6NM+（N+M）]+1=（6N+1）（6M+1）
6乘以陽性上等數加上1等於陽性上合數。
6[6NM-（N+M）]+1=（6N-1）（6M-1）
6乘以陽性下等數加上1等於陽性下合數。
在6n+1數列中只有這兩種合數，餘下就是陽性素數了，所以就有陽性素數定理
X=/=6NM+-（N+M）
陽性不等數不等於陽性上下兩式。
6X+1=P
6乘以陽性不等數加上1等於陽性素數。
與孿生素數相對應的完全不等數
(X)=/=6NM+-(M+-N)
完全不等數,它既不等於陰性上下兩式；也不等於陽性上下兩式。
6(X)+1=P
6乘以完全不等數加上1等於陽性素數；
6(X)-1=q
6乘以完全不等數減去1等於陰性素數。
一個完全不等數所產生的陰性素數q和陽性素數P就是一對孿生素數.
並且完全不等數與孿生素數是一一對應的.
四。陰陽四種等數在自然數列中的分布概況
6NM+（M-N）=陰性上等數 6NM-（M-N）=陰性下等數
6NM+（N+M）=陽性上等數 6NM-（N+M）=陽性下等數
為了搞清它們在自然數中分布情況，把四式中的N叫級別因子數，M叫無限因子數。
四種等數的每一個級別的最小等數都在6NN+-（N+N）範圍。
每一級別的上等數相鄰兩等數距離是6n+1，在自然數列中比例是1/（6n+1），陰陽兩種上等數每個級別的比例合計是2/（6n+1），（但實際是略少於這個比例，因每一級別的底部都沒有這個級別的等數。）
每一級別的下等數相鄰等數的距離是6n-1，在自然數列中的比例是1/（6n-1），陰陽兩種下等數的每個級別的合計比例是2/（6n-1），（但實際是略少於這個比例，因每一級別的底部都沒有這個級別的等數。）
在相對應的級別標準單位的連續自然數篩掉一個級別的四種等數後，剩下非該級別的自然數的比例是[(6N-1)(6N-3)]/[(6N+1)(6N-1)].並且是精準的。
五。四種等數大小數列的互相滲透
自然數列中在陰性方面有陰性上等數和陰性下等數兩種數列；自然數數列在陽性方面有陽性上等數和陽性下等數兩種數列。它們的級別有無限多，每一個級別的數列的等數也是無限多的。同一種等數級別不同的數列都是互相滲透而產生重疊，並以兩級別的等數相鄰距離的乘積而嚴格地滲透重疊的。
篩掉N及以下級別的所有等數用（6NN+6N）*3/5*5/7*9/11*11/13*......*(p-2)/p這個連乘式正好可以解決它們的滲透重疊關係。
四種等數數列之間都有互相滲透而重疊，只有同一級別陰陽上上數列和下下數列沒有滲透。
如第一級別的陽性下等數，從4開始每隔5個自然數就是一個第一級別的陽性下等數，它的比例是1/5，只要大於3的任何連續5個自然數，第一級別陽性下等數的比例是1/5，並且永遠不變。第一級別的陰性下等數從6開始每隔5個個自然數就是一個陰性下等數，它的比例是1/5,只要大於5的連續5個自然數，第一級別陰性下等數的1/5的比例也是永遠不變的。這樣第一級別的陰陽兩種下等數的比例是2/5，在任何大於5的5個連續自然數這個比例也是永遠不變的。第一級別的陰陽兩種上等數2/7,只要是連續7的自然數這個比例也是永遠不變的。由於上下兩等數的互相重疊，它們的比例是20/35,為什麼不是4/7,因為只有在大於7的連續35個自然數這個比例是不變的，如果連續7個自然數，它的比例有時是2/7,有時是3/7，有時是4/7.其它級別也是一樣的。
如果這個級別的等數間隔距離是合數的，這個級別的等數都與前面級別的等數重疊的，所以這些級別就不用計算了。
這樣就立出以下的計算公式：
（6NN+6N）*3/5*5/7*9/11*11/13*......*(p-2)/p
(6NN+6N)是一個自然數的大體表達式，P《=N N以內最大的素數。
六。對應數段與同步區間
- 對應數段和精準的比例
計算一個級別的四種等數，只有在同一級別的對應數段為單位才是精準的比例，不然就有誤差。
一個N級別的標準單位是（6N+1）（6N-1）；在計算N級別及以下的四種等數，它們的對應數段是N級別及以下的所有有性素數（不包括2和3的素數）的乘積。
對應數段的增大速度非常快。
對應數段的對應位置一定要在大於最大級別 的最小陰性等數。
在這位置以上任何連續的對應數段為單位的自然數中，它們的自己的等數是一定的，比例是精準的（不包括大於它的級別等數）。
以對應數段為周期，對應的陰陽上下四種等數嚴密地分布在自然數列中。
計算一個以對應數段為單位的連續自然數中的對應級別中的四種等數用這個公式是非常精準的，但不能包括比這個級別大的等數，5*7*11*13*......*P*3/5*5/7*9/11*11/13*......*(p-2)/p=大於這些級別的等數和完全不等數。
由於每一個級別底部都沒有本級別的等數和任何的標準單位中都有很多大於這些級別的等數，所以都會以掛另原因而產生誤差，從而掩蓋了這個公式的精準的實質。
2.與素數分布基本同步的SN區間
把自然數劃分成12，24，36……以12為遞增的一個個區間，這樣的區間叫SN區間。即:
12（1+2+3+……+N）-12（1+2+3+......+(N-1)=(6N^2+6N)-[6(N-1)^2+6(N-1)]=12N
SN區間與四種等數分布是同步的。
在這樣的區間內包括N級別及以下的所有四種等數數列的等數，並沒有比N級別大的數列等數，與四種等數的級別是完全同步的，所以與素數的分布也是同步的。
七。每個大於S8區間內都有8個以上的完全不等數
在每一個SN區間只有存在1至N級別的四種數列等數，每一級別等數的比例是可以確定，由於上下級別的滲透。就可以拿以下式來計算S8區間的完全不等數的至少個數。
12*8*11/35*95/143*251/323*479/575*779/899*1151/1295*1593/1763*2111/2303=8.2768
（由於計算的區間不是對應的標準單位，肯定會有誤差，為保險起見，把各級別中合數也給算上，一個級別中上下兩種等數的重疊則沒有算。）
其他每一個SN區間可用這種方法計算.
隨著區間的增大完全不等數計算的數量也會越來越多.以後都會超過8個.
誤差分析
在計算任何區間的等數，由於標準的比例與計算的區間都不能整除，所以存在誤差是一定，由於誤差掩蓋了等數的精準比例。
由於各個區間與相對應的標準單位不能同步，一個級別及以下的所有有性素數的乘積為這個級別的對應的標準單位，一個標準單位比對應的級別區間大得很多，如第一和第二兩個級別的標準單位就有5005，第二個N區間只有24，在5005的連續自然數中就有許多比第二級別大得多的等數，所以計算出的數值大多會有誤差。只有用標準的單位計算相對應的所有級別的等數才不會有誤差，由於標準單位的增速比等數級別快得多，所以就沒有所有等數級別的標準區間。
另外，可用最嚴格下取整的誤差分析方法，將SN區間捆綁成1,2,4,8,16......2^(N-1)的LN區間.在每一個大於S8的SN區間計算都大於8個完全不等數,在每一個LN區間都有2^N-1級別等數數列, 每級級別有4種等數數列,每一級別一種等數篩一次誤差極限是1 .每一個LN區間誤差極限是4*(2^N-1).
8*2^(N-1)-4*(2^N-1)=4
最嚴格下取整後大於L4的區間仍然還有4個完全不等數。
總結
根據以上的論證，在大於S8區間每一個SN區間都有8個以上的完全不等數.
嚴格的下取整後，大於L4的每一個LN區間都還有多於4個的完全不等數。
LN區間是無限多的，完全不等數與孿生素數對是一一對應的，所以孿生素數也是無限多的。
這個證明期待著權威的表態。其實權威旱在二十年前就已表態，說孿生素數問題是屬於解析數論的範疇。[2]
以下是S100以內的孿生素數分布表
（以孿中為準，含3；5） N 對數 最後一對 s 1 8 73 71 s 2 7 199 197 s 3 8 433 431 s 4 7 661 659 s 5 9 1063 1061 s 6 11 1489 1487 s 7 11 1999 1997 s 8 13 2593 2591 s 9 10 3169 3167 s 10 19 3931 3929 s 11 19 4723 4721 s 12 14 5521 5519 s 13 15 6553 6551 s 14 20 7561 7559 s 15 14 8629 8627 s 16 18 9769 9767 s 17 18 10939 10937 s 18 20 12253 12251 s 19 11 13681 13679 s 20 20 14869 14867 s 21 20 16633 16631 s 22 28 18133 18131 s 23 19 19843 19841 s 24 29 21601 21599 s 25 26 23371 23369 s 26 16 25171 25169 s 27 23 27109 27107 s 28 28 29209 29207 s 29 23 31321 31319 s 30 32 33349 33347 s 31 30 35593 35591 s 32 25 37993 37991 s 33 23 40153 40151 s 34 28 42841 42839 s 35 28 45343 45341 s 36 25 47809 47807 s 37 37 50593 50591 s 38 30 53281 53279 s 39 26 56101 56099 s 40 34 59023 59021 s 41 25 61981 61979 s 42 27 64921 64919 s 43 31 68113 68111 s 44 37 71263 71261 s 45 32 74509 74507 s 46 33 77713 77711 s 47 37 81199 81197 s 48 37 84631 84629 s 49 38 88003 88001 s 50 35 91573 91571 s 51 43 95443 95441 s 52 41 99139 99137 s 53 34 102931 102929 s 54 39 106861 106859 s 55 36 110881 110879 s 56 40 114799 114797 s 57 43 118903 118901 s 58 46 122869 122867 s 59 34 127291 127289 s 60 42 131713 131711 s 61 44 136069 136067 s 62 35 140551 140549 s 63 40 145009 145007 s 64 47 149731 149729 s 65 51 154279 154277 s 66 43 159193 159191 s 67 46 163993 163991 s 68 36 168901 168899 s 69 37 173779 173777 s 70 55 178909 178907 s 71 56 183973 183971 s 72 44 189151 189149 s 73 46 194269 194267 s 74 46 199753 199751 s 75 47 205033 205031 s 76 53 210601 210599 s 77 34 215983 215981 s 78 53 221719 221717 s 79 51 227473 227471 s 80 55 233161 233159 s 81 47 238921 238919 s 82 42 244861 244859 s 83 54 250969 250967 s 84 47 256903 256901 s 85 45 262783 262781 s 86 65 269221 269219 s 87 50 275593 275591 s 88 51 281923 281921 s 89 55 288361 288359 s 90 46 294649 294647 s 91 56 301363 301361 s 92 56 307873 307871 s 93 59 314599 314597 s 94 61 321469 321467 s 95 72 328129 328127 s 96 59 335173 335171 s 97 45 342073 342071 s 98 56 349081 349079 s 99 56 356263 356261 s 100 61 363439 363437 s 101 44 370873 370871 |
36N（N+1）+ -1形的孿生素數，N《100000000 有109128對。證明在雁盪山孿生素數詞條。
計算孿生素數個數的公式
N/6*3/5*5/7*9/11*11/13*......*(p-2)/p=M
N自然數，P是少於或等於N/36平方根乘以6的素數，M是孿生素數個數。
由於每一個級別的底部都沒有等數，計算出的數值都比實際少。如果取所屬級別的對應數段，不篩大於這些級別的等數，計算出的數值是0誤差的。
最大值
目前已知最大的孿生素數共有388,342位數，通過分散式計算項目Primegrid的Sophie Germain素數搜尋項目於2016年9月14日發現：
2,996,863,034,895×21,290,000±1
非估算性
如果也能證明這個和比任何數都大，就證明了孿生素數有無窮多個了。這個想法很好，可是事實卻違背了布隆的意願。他證明了這個倒數和是一個有限數，這個常數就被稱為布隆常數：b=1.90216054…布隆還發現，對於任何一個給定的整數m，都可以找到m個相鄰素數，其中沒有一個孿生素數。
1920年代，通過使用著名的篩理論（Sieve theory，基於埃拉托斯特尼篩法的理論），挪威的維果·布朗（Viggo Brun）證明了2能表示成兩個最多有9個素數因子的數的差。這個結論已經有些近似於孿生素數猜想了。可以看到，只要將這個證明中的“最多有9個素數因子的數”改進到“最多有1個素數因子的數”，就可以證明孿生素數猜想了。
1966年由已故的我國數學家陳景潤利用篩法（sieve method）所取得的。陳景潤證明了：存在無窮多個素數p，使得p+2要么是素數，要么是兩個素數的乘積。這個結果與他關於 Goldbach 猜想的結果很類似。一般認為，由於篩法本身的局限性，這一結果在篩法範圍內很難被超越。
2013年5月13日，張益唐在美國哈佛大學發表主題演講，介紹了他的這項研究進展。《自然》的報導稱，如果這個結果成立，就是第一次有人正式證明存在無窮多組間距小於定值的素數對。換言之，張益唐將給孿生素數猜想證明開一個真正的“頭”。世界頂級數學期刊《數學年刊》（Annals of Mathematics）將準備接受張益唐作出證明的這篇文章，審稿人還評價“其證明是對的，並且是一流的數學工作”。
張益唐的論文在5月14號在網路上公開，兩個星期後的5月28號，這個常數下降到了6000萬。僅僅過了兩天的5月31號，下降到了4200萬。又過了三天的6月2號，則是1300萬。次日，500萬。6月5號，40萬。在英國數學家Tim Gowers等人發起的“Polymath”計畫中，孿生素數問題成為了一個在全球數學工作者中利用網路進行合作的一個典型。人們不斷的改進張益唐的證明，進一步拉近了與最終解決孿生素數猜想的距離。截至2014年10月9日 (2014-10-09)[update], 素數對之差被縮小為 ≤ 246。從246到2，雖然離孿生質數的桂冠近在咫尺，但道路越來越艱難，誰能摘冠、何時摘冠不得而知。
估算性
證明孿生素數猜想的另一類結果則是估算性結果。 這類結果估算的是相鄰素數之間的最小間隔Δ， 更確切地說是：
翻譯成白話文， 這個表達式所定義的是兩個相鄰素數之間的間隔， 與其中較小的那個素數的對數值之比在整個素數集合中所取的最小值。 很顯然， 孿生素數猜想如果成立， 那么Δ必須等於 0。因為孿生素數猜想表明pn+1-pn=2對無窮多個n成立，而ln(pn)→∞，因此兩者之比的最小值對於孿生素數集合（從而對於整個素數集合也）趨於零。不過要注意，Δ=0隻是孿生素數猜想成立的必要條件，而不是充份條件。換句話說，如果能證明Δ≠0，則孿生素數猜想就不成立；但證明Δ=0卻並不意味著孿生素數猜想就一定成立。
對Δ最簡單的估算來自於素數定理。按照素數定理，對於足夠大的x，在x附近素數出現的幾率為
， 這表明素數之間的平均間隔為ln(x)（這也正是Δ的表達式中出現 ln(pn)的原因），從而
給出的其實是相鄰素數之間的間隔與平均間隔的比值，其平均值顯然為1。平均值為 1， 最小值顯然是小於等於 1， 因此素數定理給出Δ≤1。
對Δ的進一步估算始於Hardy和Littlewood。一九二六年，他們運用圓法（circle method）證明了假如廣義Riemann猜想成立，則Δ≤2/3。這一結果後來被Rankin改進為Δ≤3/5。但這兩個結果都有賴於本身尚未得到證明的廣義Riemann猜想， 因此只能算是有條件的結果。一九四零年，Erdös利用篩法首先給出了一個不帶條件的結果：Δ<1（即把素數定理給出的結果中的等號部分去掉了）。此後Ricci於一九五五年，Bombieri和Davenport於一九六六年，Huxley於一九七七年，分別把這一結果推進到Δ≤15/16，Δ≤(2+√3)/8≈0.4665及 Δ≤0.4425。Goldston和Yildirim之前最好的結果是Maier在一九八六年取得的Δ≤0.2486。
2003年，Goldston和Yildirim發表了一篇論文，聲稱證明了Δ=0。但2003年4月23日，Andrew Granville （University de Montreal）和Kannan Soundararajan（University of Michigan）發現了Goldston和Yildirim證明中的一個錯誤。2005年，他們與Janos Pintz合作完成了證明。此外，若Elliott-Halberstam猜想成立，孿生素數猜想的弱化版本——存在無窮多對相距16的素數——在Δ=0時也會成立。
Δ=0被證明後人們的注意力自然就轉到了研究Δ趨於0的方式上來。 孿生素數猜想要求Δ ~ [log(pn)]（因為pn+1-pn=2對無窮多個n成立)。Goldston和Yildirim的證明所給出的則是 Δ ~ [log(pn)]，兩者之間還有相當距離。 但是看過Goldston和Yildirim手稿的一些數學家認為，Goldston和Yildirim所用的方法存在改進的空間。這就是說，他們的方法有可能可以對Δ趨於0的方式作出更強的估計。因此Goldston和Yildirim的證明， 其價值不僅僅在於結果本身，更在於它很有可能成為未來一系列研究的起點。
其他方式
1849年，阿爾方·德·波利尼亞克提出了更一般的猜想：對所有自然數k，存在無窮多個素數對(p,p+2k)。k=1的情況就是孿生素數猜想。因此，波利尼亞克有時也被認為是孿生素數猜想的提出者。
其中的常數是所謂的孿生素數常數，其中的p表示素數。
哈代和李特爾伍德的猜測實際上是存在已久的孿生素數猜想的加強版。孿生素數猜想是指“孿生素數有無窮多個”。這個猜想至今仍未被證明。然而，哈代和李特爾伍德的猜測並不是需要建立在孿生素數猜想成立的前提上。
