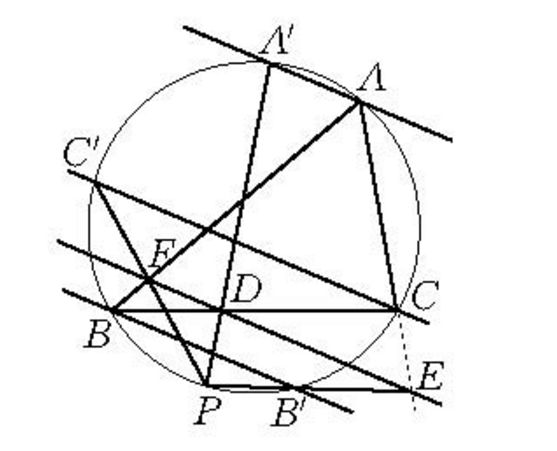
奧倍爾定理(Auber theorem)是關於共線點的一個定理,通過△ABC的三頂點引互相平行的三條直線,它們和△ABC外接圓的交點分別為A′,B′,C′,若在△ABC外接圓上取一點P,設PA′,PB′,PC′與△ABC的三邊BC,CA,AB或其延長線的交點分別為D,E,F,則D,E,F三點在同一條直線上。
基本介紹
- 中文名:奧倍爾定理
- 外文名:Auber theorem
- 所屬學科:數學
- 所屬問題:平面幾何(共線問題)
- 簡介:關於共線點的一個定理
基本介紹,定理的證明,
基本介紹
通過△ABC的項點A、B、C引互相平行的三條直線,設它們和△ABC的外接圓的交點分別為A’、B'、C',在△ABC的外接圓周上取一點P,設PA'、PB'、PC'與△ABC的三邊BC、CA、AC或其延長線的交點分別為D、E、F,則D、E、F三點在同一直線上(圖1)。
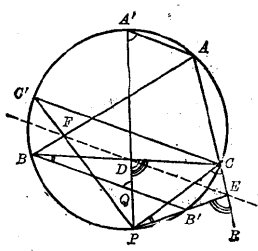 圖1
圖1定理的證明
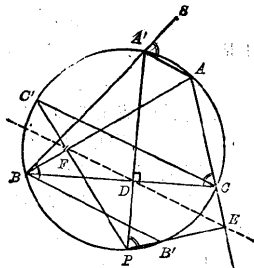 圖2
圖2首先請注意,因為A、A'、P、C四點在同一圓周上,所以
∠PCE=∠AA'P, (1)
其次,因為AA'//BB',如果設PA'和BB'的交點為Q,則有
∠AA'P= ∠BQD.
從這兩個式子,有
∠PCE=∠ BQD.
另一方面,因為∠CPE和∠CBB'是同一弦CB'所對的圓周角,所以
∠CPE=∠CBB'.
將這兩式相加,
∠PCE+∠CPE=∠BQD + /CBB',
即如把CE的延長線記作CER,則
∠PER=∠PDC.
這說明P、D、C、E四點在同一圓周上,由此,
∠PCE=∠ PDE. (2)
從(1)、(2)兩式,有
∠AA'P=∠PDE.
這表示AA' // DE。完全同樣地,可以證明AA' //DF,據此,D、E、F三點在同一直線上。
另外,在奧倍爾定理中,假設有PA'⊥BC 成立(圖2)。這時,如設BA'的延長線為BA'S,因為AA'// BB',所以
∠SA'A=∠A'BB'.
但是因為A'、B、C、A四點在同一圓周上,所以
∠SA'A=∠ACB.
又因為∠A'BB'和∠A'PB'是同一弦A'B'所對的圓周角,所以
∠A'BB'=∠A'PB',
於是
∠ACB=∠A'PB'.
這個式子表示P、D、C、E四點在同一圓周上。但因為∠PDC=∠R,所以∠PEC=∠R。
同理可證∠PFB=∠R。
於是,在PA'⊥BC的情形,奧倍爾定理成為西摩松定理。