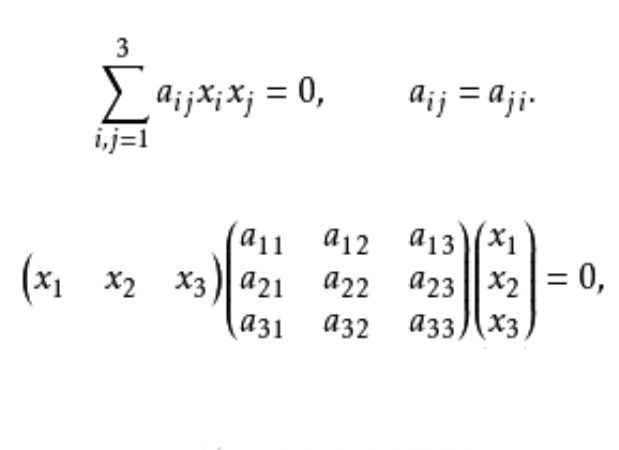奇異二次曲線(singular quadratic curve)是二次曲線的特殊類型,若二次曲線是由兩條直線構成的,則稱為奇異的或退化的二次曲線。否則稱為非奇異的或非退化的二次曲線。
基本介紹
- 中文名:奇異二次曲線
- 外文名:singular quadratic curve
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 簡介:二次曲線是由兩條直線構成的
基本介紹,相關介紹,
基本介紹
若二次曲線是由兩條直線構成的,則稱為奇異的或退化的二次曲線,否則稱為非奇異的或非退化的二次曲線。如果曲線方程為:


相關介紹
二次曲線與無窮遠直線的相關位置
在仿射平面上,齊次仿射坐標 滿足三元二次方程
滿足三元二次方程


方程(1)可簡寫成

當 時,則此二次曲線叫做非退化的二次曲線;當
時,則此二次曲線叫做非退化的二次曲線;當 時,此二次曲線叫做退化的二次曲線。
時,此二次曲線叫做退化的二次曲線。


現在求無窮遠直線 與二次曲線的交點,把
與二次曲線的交點,把 代入方程(1),得
代入方程(1),得




因此,當 時,方程(2)有兩個不相等的實根;
時,方程(2)有兩個不相等的實根;

當 時,方程(2)有兩個相等的實根;
時,方程(2)有兩個相等的實根;

當 時,方程(2)有兩個共軛的虛根。
時,方程(2)有兩個共軛的虛根。

根據二次曲線與無窮遠直線相交的情況,即根據 的符號,我們把式(1)所表示的二次曲線進行分類。
的符號,我們把式(1)所表示的二次曲線進行分類。

定義 當A33>0時,方程(1)所表示的曲線叫做橢圓型二次曲線;當A33=0時,方程(1)所表示的曲線叫做拋物型二次曲線;當A33<0時,方程(1)所表示的曲線叫做雙曲型二次曲線。而且,當 時,上述三種類型的二次曲線分別叫做橢圓、拋物線、雙曲線。
時,上述三種類型的二次曲線分別叫做橢圓、拋物線、雙曲線。

由定義,顯然雙曲線與無窮遠直線有兩個實交點(即相割),拋物線與無窮遠直線只有一個實交點(即相切),橢圓與無窮遠直線有兩個共軛虛交點(即通常意義下的相離),我們把二次曲線與無窮遠直線的交點叫做二次曲線上的無窮遠點。3種二次曲線與無窮遠直線的位置關係如圖1所示。
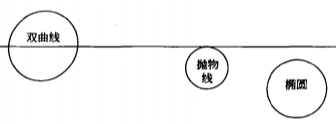
圖1
由定義顯然可知,一條非退化二次曲線為拋物線的充要條件是它與無窮遠直線相切。
二次曲線的射影分類
射影平面上二次曲線與下列五種曲線之一射影等價:
(1)  (無圖形)
(無圖形)

(2) (橢圓、雙曲線、拋物線)
(橢圓、雙曲線、拋物線)

(3) (一點)
(一點)

(4)  (一對相交直線)
(一對相交直線)

(5)  (一對重合直線)
(一對重合直線)

其中前兩類是非退化的二次曲線,後三類是退化的二次曲線。