奇偶校驗碼是一種增加二進制傳輸系統最小距離的簡單和廣泛採用的方法。是一種通過增加冗餘位使得碼字中"1"的個數恆為奇數或偶數的編碼方法,它是一種檢錯碼。在實際使用時又可分為垂直奇偶校驗、水平奇偶校驗和水平垂直奇偶校驗等幾種。
基本介紹
- 中文名:奇偶校驗碼
- 分類:垂直、水平、水平垂直奇偶校驗等
基本概念
奇偶校驗碼
碼距
基本分類:
垂直奇偶校驗
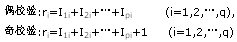

水平奇偶校驗
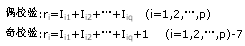

水平垂直奇偶校驗


奇偶校驗碼原理


奇偶校驗碼是一種增加二進制傳輸系統最小距離的簡單和廣泛採用的方法。是一種通過增加冗餘位使得碼字中"1"的個數恆為奇數或偶數的編碼方法,它是一種檢錯碼。在實際使用時又可分為垂直奇偶校驗、水平奇偶校驗和水平垂直奇偶校驗等幾種。
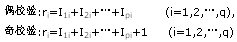

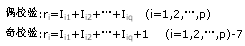




奇偶校驗碼是一種增加二進制傳輸系統最小距離的簡單和廣泛採用的方法。是一種通過增加冗餘位使得碼字中"1"的個數恆為奇數或偶數的編碼方法,它是一種檢錯碼。在...
奇偶校驗(Parity Check)是一種校驗代碼傳輸正確性的方法。根據被傳輸的一組二進制代碼的數位中“1”的個數是奇數或偶數來進行校驗。採用奇數的稱為奇校驗,反之,...
奇偶校驗位 (Parity)多被套用於計算機硬體的錯誤檢測中。奇偶校驗通常用在數據通信中來保證數據的有效性。每個設備必須決定是否它將被用為偶校驗、奇校驗、或非校驗...
奇偶校驗法常用於識別數據是否發生傳輸錯誤,並且可以啟動校正措施,或者捨棄傳輸發生錯誤的數據,要求重新傳輸有錯誤的數據塊。...
為了檢驗這種錯誤,常採用奇偶校驗的方法。即在原二進制信息碼組後添加一位檢驗位(監督碼元),使得添加校驗位碼元後整個碼組中1碼元的個數為奇數或偶數。若為奇數,...
二維奇偶校驗碼不僅可用來檢錯,還可用來糾正一些錯碼。例如,當碼組中僅在一行中有奇數個錯誤時,則能夠確定錯碼位置,從而糾正它。...
單向奇偶校驗(Row Parity)由於一次只採用單個校驗位,因此又稱為單個位奇偶校驗(Single Bit Parity)。傳送器在數據禎每個字元的信號位後添一個奇偶校驗位...
循環冗餘校驗碼(CRC),簡稱循環碼,是一種常用的、具有檢錯、糾錯能力的校驗碼,在早期的通信中運用廣泛。循環冗餘校驗碼常用於外存儲器和計算機同步通信的數據校驗。...
crc校驗 奇偶校驗 校驗碼 md5校驗器 md5校驗 md5校驗工具 md5校驗碼 校驗儀 校驗(校證)核對查考;比較驗證。 唐李綽《尚書故實》:“﹝汲冢書﹞竹簡漆書科斗...
是一種編碼。指在傳輸過程中發生錯誤後,在接收端能自動檢查並發現錯誤的編碼。目前常用的檢錯碼有奇偶校驗碼、恆比碼等。...
檢錯碼是一種編碼,指在傳輸過程中發生錯誤後,在接收端能自動檢查並發現錯誤的編碼.目前常用的檢錯碼有奇偶校驗碼、恆比碼等。...
LDPC碼是麻省理工學院Robert Gallager於1963年在博士論文中提出的一種具有稀疏校驗矩陣的分組糾錯碼。幾乎適用於所有的信道,因此成為編碼界近年來的研究熱點。它的性能...
編碼理論檢錯碼 有發現錯誤能力的碼稱為檢錯碼。常用的檢錯碼有奇偶校驗碼和等重碼。採用檢錯碼的通信系統要有反饋通道,當發現收到的信號有錯誤時,通過反饋通道...
