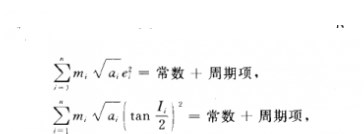式中m;,a;,e;,l，分別為第i個大行星的質量、軌道半長徑、偏心率、軌道傾角，n為大行星個數.此二式表明太陽系是穩定的，但他們的這個結果，只考慮了行星間引力的一階攝動，只能是粗略結論.在二階攝動基礎上，泊松(Poisson , S. -D.)得到一個定理:大行星軌道半長徑沒有長期變化，即不會隨時間增加而無限增大或縮小.這只是從一個側面說明太陽系可能是穩定的.在高階攝動基礎上，不少人曾得出行星道半長徑有長期變化的結果.但到1982年，梅塞奇(Message,P. J.)終於證明了在任意階攝動下，大行星軌道半長徑仍沒有長期變化.儘管這個定理很重要，但也只能說明太陽系可能是穩定的，因為若某行星軌道偏心率如增加到大1，仍會出現逃逸而不穩定.卡姆理論出現
基本介紹
中文名：太陽系的穩定
外文名：taiyangxidewenfing
太陽系的穩定性(07題(problem on the stabilityof solar system)天體力學中的一個基本問題.研究太陽系在自身引力作用下是否能保持現在的狀態，即各行星順序不變，軌道形狀和大小大體接近現在情況;有無大行星逃逸或碰撞甚至墮落到太陽上.這是天體力學定性理論和天體演化學的一個基本問題.雖然已研究了三百年，但至今仍未解決.牛頓時代雖有研究，但未給出具體結果.第一個用理論給出太陽系穩定性結論的是18世紀的拉普拉斯(Laplace, P. -S.)和拉格朗日(Lagrange, J. -L. )，這就是後來以他們二人名字命名的定理，用公式表示為 式中m;,a;,e;,l，分別為第i個大行星的質量、軌道半長徑、偏心率、軌道傾角，n為大行星個數.此二式表明太陽系是穩定的，但他們的這個結果，只考慮了行星間引力的一階攝動，只能是粗略結論.在二階攝動基礎上，泊松(Poisson , S. -D.)得到一個定理:大行星軌道半長徑沒有長期變化，即不會隨時間增加而無限增大或縮小.這只是從一個側面說明太陽系可能是穩定的.在高階攝動基礎上，不少人曾得出行星道半長徑有長期變化的結果.但到1982年，梅塞奇(Message,P. J.)終於證明了在任意階攝動下，大行星軌道半長徑仍沒有長期變化.儘管這個定理很重要，但也只能說明太陽系可能是穩定的，因為若某行星軌道偏心率如增加到大1，仍會出現逃逸而不穩定.卡姆理論出現後，用於研究太陽系這個動力系統，從機率意義上得到有關太陽系穩定性的一個定理，稱為阿諾爾德定理:若太陽系各行星質量(以太陽質量為1)、軌道偏心率、軌道傾角都是小量，則在行星相互引力作用下，各行星的運動幾乎永遠是擬周期軌道，即保持在很細的環面上.定理中的所謂“幾乎”，表示不是擬周期軌道的機率為0，也就是說可認為太陽系幾乎是穩定的.當然，行星質量等於小量，是否符合太陽系實際，還很難判定，因此，還不能最後肯定太陽系是穩定的。近年來由於計算機水平不斷提高，用數值方法研究太陽系的穩定性成為可能，形成了太陽系穩定性的數值探索這個新領域.現在已有五個研究組在進行探索，其中美國兩個，英、法、日各一個一般都是採用太陽系質心中大行星運動的平均化方程，用數值方法計算各大行星軌道根數a，。,1，的變化，若沒有長期變化或振幅很大的長周期變化，則判定太陽係為穩定的.現在都已算到幾千萬甚至1億年的時間範圍，看來結果都表明太陽係為穩定的.但法國經度局的一研究組計算各大行星運動的李亞普諾夫特徵數(I_CN)接近於0. 2，表明太陽系在時間趨於無窮時為混沌狀態，即為不穩定情況.當然這都還不是最後結論，有待進一步研究.
